题目内容
4.等腰△ABC的角A=$\frac{π}{3}$,|BC|=2,以A为圆心,$\sqrt{3}$为半径作圆,MN为该圆的一条直径,则$\overrightarrow{BM}•\overrightarrow{CN}$的最大值为2$\sqrt{3}$-1.分析 利用平面向量的三角形法则,进行数量积的运算,得到关于夹角θ的余弦函数解析式,借助于有界性求最值即可.
解答  解:设$\overrightarrow{CB}$与$\overrightarrow{AM}$的夹角为θ,
解:设$\overrightarrow{CB}$与$\overrightarrow{AM}$的夹角为θ,
∴$\overrightarrow{BM}•\overrightarrow{CN}$=($\overrightarrow{BA}$+$\overrightarrow{AM}$)•($\overrightarrow{CA}$+$\overrightarrow{AN}$)=$\overrightarrow{BA}$•$\overrightarrow{CA}$+$\overrightarrow{AM}$•($\overrightarrow{CA}$-$\overrightarrow{BA}$)-${\overrightarrow{AM}}^{2}$=2×2×$\frac{1}{2}$+$\overrightarrow{CB}$•$\overrightarrow{AM}$-3=2$\sqrt{3}$cosθ-1≤2$\sqrt{3}$-1
故答案为:$2\sqrt{3}-1$
点评 本题考查了平面向量的数量积运算,借助于余弦函数的有界性求最值;属于中档题.

练习册系列答案
相关题目
9.已知集合$M=\left\{{x\left|{\frac{x-2}{x-3}<0}\right.}\right\},N=\left\{{x\left|{{{log}_{\frac{1}{2}}}(x-2)≥1}\right.}\right\}$,则M∩N=( )
| A. | $[{\frac{5}{2},3})$ | B. | $({2,\frac{5}{2}}]$ | C. | $[{2,\frac{5}{2}}]$ | D. | $({\frac{5}{2},3})$ |
13.若直线ax+by+1=0(a>0,b>0)把圆(x+4)2+(y+1)2=16分成面积相等的两部分,则$\frac{1}{2a}+\frac{2}{b}$的最小值为( )
| A. | 10 | B. | 8 | C. | 5 | D. | 4 |
14.若复数z满足i(z-1)=1+i(i虚数单位),则z=( )
| A. | 2-i | B. | 2+i | C. | 1-2i | D. | 1+2i |
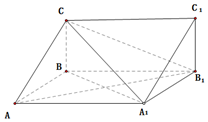 如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.
如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.