题目内容
6.在区间[0,2]内随机取出两个数,则这两个数的平方和在区间[0,2]内的概率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{8}$ |
分析 首先分析题目求这两个数的平方和也在区间[0,2]内的概率,可以联想到用几何的方法求解,利用面积的比值直接求得结果.
解答 解:将取出的两个数分别用x,y表示,则x,y∈[0,2]
要求这两个数的平方和也在区间[0,2]内,即要求0≤x2+y2≤2,
故此题可以转化为求0≤x2+y2≤2在区域$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$内的面积比的问题.
即由几何知识可得到概率为$\frac{\frac{1}{4}π•2}{{2}^{2}}$=$\frac{π}{8}$;
故选:D.
点评 此题考查等可能时间概率的问题,利用几何概型的方法解决本题,概率知识在高考中难度有所下降,对利用古典概型和几何概型的基本方法要熟练掌握.

练习册系列答案
相关题目
1.已知Rt△ABC中,AB=3,AC=1,$∠A=\frac{π}{2}$,以B,C为焦点的双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)经过点A,且与AB边交于点D,若$\frac{{|{AD}|}}{{|{BD}|}}$的值为( )
| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{9}{2}$ | D. | 4 |
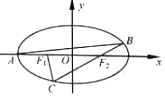 如图,设点A,F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左,右焦点,过点A作斜率为k的直线交椭圆于另一点B,连接BF2并延长交椭圆于点C.
如图,设点A,F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左,右焦点,过点A作斜率为k的直线交椭圆于另一点B,连接BF2并延长交椭圆于点C.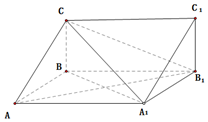 如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.
如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.