题目内容
5.已知集合A={1,2,3,4},集合B={x|x2-2x<0},则集合A∩B中元素的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先求出集合A、集合B,从而求出集合A∩B,由此能求出集合A∩B中元素的个数.
解答 解:∵集合A={1,2,3,4},
集合B={x|x2-2x<0}={x|0<x<2},
∴集合A∩B={1}.
∴集合A∩B中元素的个数为1.
故选:A.
点评 本题考查交集中元素个数的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
相关题目
13.若直线ax+by+1=0(a>0,b>0)把圆(x+4)2+(y+1)2=16分成面积相等的两部分,则$\frac{1}{2a}+\frac{2}{b}$的最小值为( )
| A. | 10 | B. | 8 | C. | 5 | D. | 4 |
10.已知a∈R,若$f(x)=(\frac{1}{x}+a){e^x}$在区间(0,1)上有且只有一个极值点,则a的取值范围是( )
| A. | a<0 | B. | a>0 | C. | a≤1 | D. | a≥0 |
17.复数$\frac{2}{i(3-i)}$=( )
| A. | $\frac{1-3i}{5}$ | B. | $\frac{1+3i}{5}$ | C. | $\frac{3+i}{5}$ | D. | $\frac{3-i}{5}$ |
14.若复数z满足i(z-1)=1+i(i虚数单位),则z=( )
| A. | 2-i | B. | 2+i | C. | 1-2i | D. | 1+2i |
15.若集合M={1,3},N={1,3,5},则满足M∪X=N的集合X的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
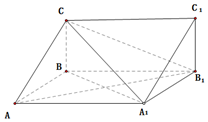 如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.
如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.