题目内容
16.已知f(x)是R上可导的增函数,g(x)是R上可导的奇函数,对?x1,x2∈R都有|g(x1)+g(x2)|≥|f(x1)+f(x2)|成立,等差数列{an}的前n项和为Sn,f(x)同时满足下列两件条件:f(a2-1)=1,f(a9-1)=-1,则S10的值为10.分析 根据题意,令x1=-x2有|g(x1)+g(-x1)|≥|f(x1)+f(-x1)|,结合g(x)的奇偶性可得|f(x1)+f(-x1)|≤0,分析可得f(x)为奇函数;又由f(a2-1)=1,f(a9-1)=-1,分析可得则有a2+a9=2,由等差数列前n项和公式计算可得答案.
解答 解:根据题意,对?x1,x2∈R都有|g(x1)+g(x2)|≥|f(x1)+f(x2)|成立,
令x1=-x2有:|g(x1)+g(-x1)|≥|f(x1)+f(-x1)|,
又由g(x)是R上可导的奇函数,
则有|f(x1)+f(-x1)|≤0,
即f(x1)+f(-x1)=0,
故函数f(x)为奇函数;
若f(a2-1)=1,f(a9-1)=-1,
则有(a2-1)+(a9-1)=0,
即a2+a9=2,
S10=$\frac{({a}_{1}+{a}_{10})×10}{2}$=$\frac{({a}_{2}+{a}_{9})×10}{2}$=10;
故答案为:10.
点评 本题考查函数的奇偶性、单调性的综合应用,涉及等差数列的性质,关键是分析函数f(x)的奇偶性.

练习册系列答案
相关题目
1.若执行如图所示的程序框图,则输出的结果k=( )
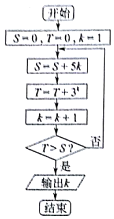

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
5.执行如图所示的程序框图,若输入的n=5,则输出的结果为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
6.已知tanα=$\frac{3}{4}$,则sin2α=( )
| A. | $-\frac{12}{25}$ | B. | $\frac{12}{25}$ | C. | $-\frac{24}{25}$ | D. | $\frac{24}{25}$ |