题目内容
8.在△ABC中,角A,B,C所对的边分别为a,b,c,已知$sin(A-B)=2{sin^2}(\frac{C}{2}-\frac{π}{4})$.(1)求sinAcosB的值;
(2)若$\frac{a}{b}=\frac{{2\sqrt{3}}}{3}$,求B.
分析 (1)由已知利用三角形内角和定理,三角函数恒等变换的应用化简可得$sinAcosB=\frac{1}{2}$;
(2)由已知利用正弦定理及(Ⅰ)可得$sin2B=\frac{{\sqrt{3}}}{2}$,进而可求B的值.
解答 解:(1)$sin(A-B)=1-cos(C-\frac{π}{2})=1-sinC=1-sin(A+B)⇒2sinAcosB=1$,
∴$sinAcosB=\frac{1}{2}$;
(2)$\frac{sinA}{sinB}=\frac{a}{b}=\frac{{2\sqrt{3}}}{3}$,由(1)知$sinAcosB=\frac{{2\sqrt{3}}}{3}sinBcosB=\frac{{\sqrt{3}}}{3}sin2B=\frac{1}{2}$,
∴$sin2B=\frac{{\sqrt{3}}}{2}$,
∴$2B=\frac{π}{3}$或$\frac{2π}{3}$,
∴$B=\frac{π}{6}$或$\frac{π}{3}$.
点评 本题主要考查了三角形内角和定理,三角函数恒等变换的应用,正弦定理在解三角形中的应用,属于基础题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
8.已知集合A={x|0≤x≤5},B={x∈N*|x-1≤2},则A∩B=( )
| A. | {x|0≤x≤3} | B. | {1,2,3} | C. | {0,1,2,3} | D. | {x|1≤x≤3} |
19.已知递增的等比数列{an}的公比为q,其前n项和Sn<0,则( )
| A. | a1<0,0<q<1 | B. | a1<0,q>1 | C. | a1>0,0<q<1 | D. | a1>0,q>1 |
13.函数$y=sin({\frac{π}{3}x+\frac{π}{6}})$的图象可由函数$y=cos\frac{π}{3}x$的图象至少向右平移m(m>0)个单位长度得到,则m=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
18.各项均不为零的等差数列{an}的前n项和为Sn,则$\frac{{S}_{5}}{{a}_{3}}$的值是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{5}{2}$ | D. | 5 |
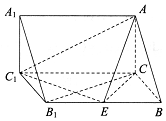 如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.
如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.