题目内容
1.若执行如图所示的程序框图,则输出的结果k=( )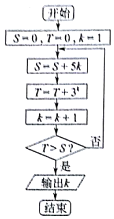
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 模拟执行程序框图,依次写出每次循环得到的S,T,k的值,当S=30,T=39时,满足条件退出循环可得输出的k的值.
解答 解:模拟程序的运行,可得
S=0,T=0,k=1
执行循环体,S=5,T=3,k=2
不满足条件T>S,执行循环体,S=15,T=12,k=3
不满足条件T>S,执行循环体,S=30,T=39,k=4
满足条件T>S,退出循环,输出k的值为4.
故选:C.
点评 本题主要考查了程序框图和算法,依次写出每次循环得到的S,T,k的值是解题的关键,属于基本知识的考查.

练习册系列答案
相关题目
12.已知定义在区间[-3,3]上的函数f(x)=2x+m满足f(2)=6,在[-3,3]上随机取一个实数x,则使得f(x)的值不小于4的概率为( )
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的渐近线与圆${({x-2\sqrt{2}})^2}+{y^2}=\frac{8}{3}$相切,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 3 |
13.函数$y=sin({\frac{π}{3}x+\frac{π}{6}})$的图象可由函数$y=cos\frac{π}{3}x$的图象至少向右平移m(m>0)个单位长度得到,则m=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |