题目内容
12.袋中装有大小相同的4个红球和6个白球,从中取出4个球.(1)若取出的球必须是两种颜色,则有多少种不同的取法?
(2)若取出的红球个数不少于白球个数,则有多少种不同的取法?
分析 (1)用间接法分析:先计算从袋子中取出4个球的取法数目,再计算并排除其中颜色相同的取法数目,即可得答案;
(2)分3种情况讨论:①、4个全部是红球,②、有3个红球,1个白球,③、有2个红球,2个白球,分别求出每种情况下的取法数目,由分类计数原理计算可得答案.
解答 解:(1)根据题意,袋中装有大小相同的4个红球和6个白球,从中取出4个,有C104=210种取法,
其中颜色相同的情况有2种:4个红球或4个白球,
若4个红球,有C44=1种取法,
若4个白球,有C64=15种取法,
则取出球必须是两种颜色的取法有210-(1+15)=194种;
(2)若取出的红球个数不少于白球个数,分3种情况讨论:
①、4个全部是红球,有C44=1种取法,
②、有3个红球,1个白球,有C43C61=24种取法,
③、有2个红球,2个白球,有C42C62=90种取法,
则一共有1+24+90=115种取法.
点评 本题考查排列、组合的综合应用,注意球与球之间只有颜色不同.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
2.与-30°终边相同的角是( )
| A. | -330° | B. | 150° | C. | 30° | D. | 330° |
3.若cos α>0,sin α<0,则角 α的终边在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.用数列归纳法证明$\frac{1}{2}+cosα+cos2α+…+cosnα=\frac{{sin(n+\frac{1}{2})α}}{{2sin\frac{α}{2}}}$时,验证n=1时,左边式子为( )
| A. | $\frac{1}{2}$ | B. | cosα | C. | $\frac{1}{2}+cosα$ | D. | $\frac{{sin\frac{3}{2}α}}{{2sin\frac{α}{2}}}$ |
8.某工厂为了对新研发的一种产品进行合理定价,将该定价按事先拟定的价格进行试销,得到如下数据:
(1)求回归直线方程$\hat y=bx+a$;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
附:$b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})}({{y_i}-\overline y})}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},a=\overline y-b\overline x$.
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(元) | 90 | 84 | 83 | 80 | 75 | 68 |
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
附:$b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})}({{y_i}-\overline y})}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},a=\overline y-b\overline x$.
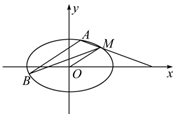 如图,已知椭圆C的中心在原点,它的一个焦点与抛物线${y^2}=4\sqrt{6}x$的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A,B两点,连接MA,MB.
如图,已知椭圆C的中心在原点,它的一个焦点与抛物线${y^2}=4\sqrt{6}x$的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A,B两点,连接MA,MB. 如图所示的三棱柱ABC-A1B1C1中,底面是正三角形,侧棱BB1⊥面ABC,D是棱BC的中点,点M在棱BB1上,且CM⊥AC1.
如图所示的三棱柱ABC-A1B1C1中,底面是正三角形,侧棱BB1⊥面ABC,D是棱BC的中点,点M在棱BB1上,且CM⊥AC1.