题目内容
已知
=19.求
的值.
| C | 1 m |
| +C | 1 n |
| C | 2 m |
| +C | 2 n |
考点:组合及组合数公式
专题:排列组合
分析:根据
=19,得出m+n=19,用n表示m,求出
的表达式即可.
| C | 1 m |
| +C | 1 n |
| C | 2 m |
| +C | 2 n |
解答:
解:∵
=19,
∴m+n=19,
∴n=19-m
∴
=
+
=
+
=m2-19m+171;
其中m、n∈N*,18≥m≥2.
| C | 1 m |
| +C | 1 n |
∴m+n=19,
∴n=19-m
∴
| C | 2 m |
| +C | 2 n |
| m(m-1) |
| 2 |
| n(n-1) |
| 2 |
=
| m(m-1) |
| 2 |
| (19-m)(18-m) |
| 2 |
=m2-19m+171;
其中m、n∈N*,18≥m≥2.
点评:本题考查了组合数公式的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知等比数列{an}中,a2a10=9,则a5+a7( )
| A、有最小值6 |
| B、有最大值6 |
| C、有最小值6或最大值-6 |
| D、有最大值-6 |
函数f(x)=(x+1)|log2x|-1的零点个数为( )
| A、1 | B、2 | C、3 | D、4 |
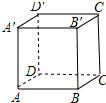 如图,正方体AC′的棱长为a.
如图,正方体AC′的棱长为a.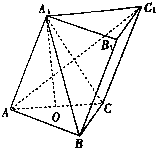 如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影O是AC的中点,BC⊥AC,四边形BCC1B1是菱形,直线AB与平面ACC1A1所成的角为45°.
如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影O是AC的中点,BC⊥AC,四边形BCC1B1是菱形,直线AB与平面ACC1A1所成的角为45°.