题目内容
已知等比数列{an}中，a2a10=9，则a5+a7（ ）
| A、有最小值6 |
| B、有最大值6 |
| C、有最小值6或最大值-6 |
| D、有最大值-6 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：由等比数列的性质可得a5a7=9，分类讨论，当a5和a7均为正、负数时，由基本不等式可得相应的最值．
解答：
解：由等比数列的性质可得a5a7=a2a10=9，
当a5和a7均为正数时，由基本不等式可得a5+a7≥2
=6，
当且仅当a5=a7=3时，a5+a7取最小值6；
当a5和a7均为负数时，由基本不等式可得a5+a7=-（-a5-a7）≤-2
=-6，
当且仅当a5=a7=-3时，a5+a7取最大值-6；
综上可得：a5+a7有最小值6或最大值-6
故选：C
当a5和a7均为正数时，由基本不等式可得a5+a7≥2
| a5a7 |
当且仅当a5=a7=3时，a5+a7取最小值6；
当a5和a7均为负数时，由基本不等式可得a5+a7=-（-a5-a7）≤-2
| a5a7 |
当且仅当a5=a7=-3时，a5+a7取最大值-6；
综上可得：a5+a7有最小值6或最大值-6
故选：C
点评：本题考查等比数列的通项公式和性质，涉及基本不等式和分类讨论的思想，属中档题．
练习册系列答案
相关题目
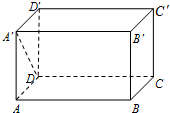如图，在长方体ABCD-A′B′C′D′中，AB=6，AA′=BC=4，则A′D与BC所成的角等于（ ）| A、30° | B、45° |
| C、60° | D、90° |
一个圆柱形容器里装有水，放在水平面上，现将容器倾斜，这时水面是一个椭圆，当圆柱的母线AB与地面所成角设a=
dx，b=
dx，c=
dx，则下列关系式成立的是（ ）
| 1 |
| 2 |
| ∫ | 2 1 |
| 1 |
| x |
| 1 |
| 3 |
| ∫ | 3 1 |
| 1 |
| x |
| 1 |
| 5 |
| ∫ | 5 1 |
| 1 |
| x |
| A、a＜b＜c |
| B、b＜a＜c |
| C、a＜c＜b |
| D、c＜a＜b |