题目内容
19.已知z=(m-1)+mi为纯虚数,则在复平面内,复数z=2-mi对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由z=(m-1)+mi为纯虚数,∴m-1=0,m≠0,解得m.利用复数的几何意义即可得出.
解答 解:由z=(m-1)+mi为纯虚数,∴m-1=0,m≠0,解得m=1.
则在复平面内,复数z=2-i对应的点(2,-1)位于第四象限.
故选:D.
点评 本题考查了复数的几何意义、方程的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
9.某同学逛书店,发现四本喜欢的书,决定至少买其中的一本,则购买方案有( )
| A. | 4种 | B. | 6种 | C. | 8种 | D. | 15种 |
9.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,$\overrightarrow{c}$=k$\overrightarrow{a}$+$\overrightarrow{b}$(k∈R),$\overrightarrow{d}$=$\overrightarrow{a}$+$\overrightarrow{b}$,如果$\overrightarrow{c}$∥$\overrightarrow{d}$,那么( )
| A. | k=-1且$\overrightarrow{c}$与$\overrightarrow{d}$同向 | B. | k=-1且$\overrightarrow{c}$与$\overrightarrow{d}$反向 | C. | k=1且$\overrightarrow{c}$与$\overrightarrow{d}$同向 | D. | k=1且$\overrightarrow{c}$与$\overrightarrow{d}$反向 |
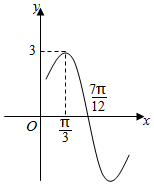 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).