题目内容
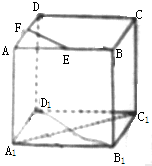
已知正方体ABCD-A1B1C1D1，E、F分别是AB、AD中点，则异面直线EF与A1C1所成的角为（ ）
| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：空间角
分析：由正方体的性质和三角形中位线定理得EF∥B1D1，由正方形性质得A1C1⊥B1D1，从而EF⊥A1C1，由此能求出异面直线EF与A1C1所成的角．
解答：
解：∵正方体ABCD-A1B1C1D1，∴BD∥B1D1，
∵E、F分别是AB、AD中点，∴EF∥BD，
∴EF∥B1D1，
∵A1B1C1D1是正方形，∴A1C1⊥B1D1，
∴EF⊥A1C1，
∴EF与A1C1所成的角为90°．
故选：D．
∵E、F分别是AB、AD中点，∴EF∥BD，
∴EF∥B1D1，
∵A1B1C1D1是正方形，∴A1C1⊥B1D1，
∴EF⊥A1C1，
∴EF与A1C1所成的角为90°．
故选：D．
点评：本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意平行公理、线面关系的合理运用．
练习册系列答案
相关题目
如果直线l⊥平面α，①若直线m⊥l，则m∥α；②若m⊥α，则m∥l；③若m∥α，则m⊥l；④若m∥l，则m⊥α，上述判断正确的是 （ ）
| A、①②③ | B、②③④ |
| C、①③④ | D、②④ |
若几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、π |
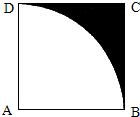如图，在边长为1的正方形ABCD中，以A为圆心，AB为半径作扇形ABD，在该正方形内随机取一点，则此点取自阴影部分的概率是