题目内容
已知长度分别为1、2、3、4、6的5根小棒,只可拼接不可折断,将这5根小棒拼接成一个三角形,当这个三角形的面积最大时,则最大角的余弦值为 .
考点:余弦定理
专题:压轴题,解三角形
分析:所求三角形的周长是肯定的,在周长一定的情况下,正三角形的面积最大,周长为16,那么最好每条边都是
,而那是不可能的,所以尽量往这种情况凑.因为只有5根,所以“6”肯定作为一条边,剩下1234,一看就知道1+4,和3+2分别为另两边时面积最大.
| 16 |
| 3 |
解答:
解:最大三角形的边长应为6,5,5,
∴由余弦定理可得:最大角的余弦值=
=
.
故答案为:
.
∴由余弦定理可得:最大角的余弦值=
| 52+52-62 |
| 2×5×5 |
| 7 |
| 25 |
故答案为:
| 7 |
| 25 |
点评:本题主要考查了学生构建三角形的能力和探究能力,考查了转化思想,属于难题.

练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1,E、F分别是AB、AD中点,则异面直线EF与A1C1所成的角为( )
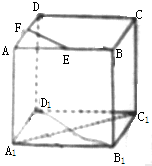

| A、30° | B、45° |
| C、60° | D、90° |
若m>n>0,则下列不等式正确的是( )
| A、2m<2n | ||||
| B、log0.2m>log0.2n | ||||
| C、am>an(0<a<1) | ||||
D、m-
|
已知x,y满足约束条件
,则z=3x+5y的最大值为( )
|
| A、0 | B、5 | C、3 | D、17 |
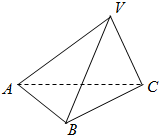 如图,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,已知其正视图的面积为2
如图,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,已知其正视图的面积为2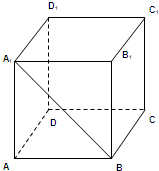 如图,ABCD-A1B1C1D1为正方体.
如图,ABCD-A1B1C1D1为正方体.