题目内容
3.若(1-2015x)2015=a0+a1x+…+a2015x2015(x∈R),则$\frac{a_1}{2015}$+$\frac{a_2}{2015^2}$+…+$\frac{a_{2015}}{2015^{2015}}$的值为-1.分析 由条件利用二项展开式的通项公式,求得a1、a2、a3、…、a2015,的值,可得要求式子的值.
解答 解:由题意可得a1=${C}_{2015}^{1}$•(-2015),a2=${C}_{2015}^{2}$•(-2015)2,a3=${C}_{2015}^{3}$•(-2015)3,…,
a2015=${C}_{2015}^{2015}$•(-2015)2015,
∴$\frac{a_1}{2015}$+$\frac{a_2}{2015^2}$+…+$\frac{a_{2015}}{2015^{2015}}$=-${C}_{2015}^{1}$+${C}_{2015}^{2}$-${C}_{2015}^{3}$+…+(-${C}_{2015}^{2015}$)
=[1-${C}_{2015}^{1}$+${C}_{2015}^{2}$-${C}_{2015}^{3}$+…+(-${C}_{2015}^{2015}$)]-1
=(1-1)2015-1=-1,
故答案为:-1.
点评 本题主要考查二项展开式的通项公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列函数中,在区间[0,+∞)上为增函数的是( )
| A. | y=-x2 | B. | y=(x-1)2 | C. | y=$\frac{1}{x}$ | D. | y=$\frac{1}{3}$x |
14.执行如图所示的程序框图,输出的S值是( )
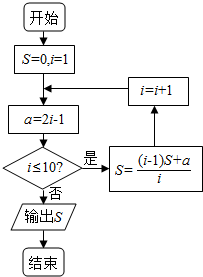

| A. | 10 | B. | 20 | C. | 100 | D. | 120 |
11.下列函数中,与函数y=-|x|的奇偶性相同,且在(-∞,0)上单调性也相同的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-$\frac{1}{|x|}$ | C. | y=1-x2 | D. | y=x2-1 |
18.直线y=x被圆x2+(y+2)2=4截得的弦长是( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |