题目内容
20.下列函数中,在区间[0,+∞)上为增函数的是( )| A. | y=-x2 | B. | y=(x-1)2 | C. | y=$\frac{1}{x}$ | D. | y=$\frac{1}{3}$x |
分析 根据函数单调性的性质进行判断.
解答 解:A.y=-x2在区间[0,+∞)上为减函数,不满足条件.
B.y=(x-1)2在区间[0,+∞)上不单调,不满足条件.
C.当x=0时,函数无意义,不满足条件.
D.y=$\frac{1}{3}$x在区间[0,+∞)上为增函数,满足条件.
故选:D
点评 本题主要考查函数单调性的判断,比较基础.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
10.已知集合A={1,2,3},则“a=3”是“a∈A“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既充分也不必要条件 |
8.已知下列问题:
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组;
②从甲、乙、丙三名同学中选出两名同学参加一项活动;
③从α,b,c,d四个字母中取出2个字母;
④从1,2,3,4四个数字中取出2个数字组成一个两位数.
其中是排列问题的有( )
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组;
②从甲、乙、丙三名同学中选出两名同学参加一项活动;
③从α,b,c,d四个字母中取出2个字母;
④从1,2,3,4四个数字中取出2个数字组成一个两位数.
其中是排列问题的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.已知α是第二象限角,其终边上一点$P(x,\sqrt{3})$,且$cosα=\frac{{\sqrt{2}}}{4}x$,则sinα=( )
| A. | $-\frac{{\sqrt{6}}}{4}$ | B. | $-\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
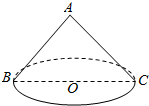 如图,已知圆锥的轴截面是腰长为$\sqrt{2}$的等腰直角三角形.试求:
如图,已知圆锥的轴截面是腰长为$\sqrt{2}$的等腰直角三角形.试求: