题目内容
7. 已知渡船在静水中速度$\overrightarrow{v_2}$的大小为$(\sqrt{6}+\sqrt{2})$m/s,河水流速$\overrightarrow{v_1}$的大小为2m/s.如图渡船船头方向与水流方向成$\frac{π}{4}$夹角,且河面垂直宽度为$600(\sqrt{3}+1)m$.
已知渡船在静水中速度$\overrightarrow{v_2}$的大小为$(\sqrt{6}+\sqrt{2})$m/s,河水流速$\overrightarrow{v_1}$的大小为2m/s.如图渡船船头方向与水流方向成$\frac{π}{4}$夹角,且河面垂直宽度为$600(\sqrt{3}+1)m$.(Ⅰ)求渡船的实际速度与水流速度的夹角;
(Ⅱ)求渡船过河所需要的时间.[提示:4+2$\sqrt{3}={(\sqrt{3}+1)^2}$].
分析 (Ⅰ)方法一:(向量坐标法)以O为坐标原点,$\overrightarrow{v_1}$所在直线为x轴建立平面直角坐标系,根据向量的坐标运算和向量的模以及夹角公式即可求出,
方法二:(正、余弦定理),根据平行四边形法则和正弦定理和余弦定理即可求出,
(Ⅱ)先求出所走的路程,即可求出所需要的时间
解答 解:(Ⅰ)方法一:(向量坐标法)
以O为坐标原点,$\overrightarrow{v_1}$所在直线为x轴建立平面直角坐标系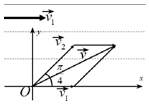
由条件$<\overrightarrow{v_1},\overrightarrow{v_2}>=\frac{π}{4}$,$|\overrightarrow{v_1}|=2$,$|\overrightarrow{v_2}|=\sqrt{6}+\sqrt{2}$
知$\overrightarrow{v_1}=(2,0)$,$\overrightarrow{v_2}=(\sqrt{3}+1,\sqrt{3}+1)$,
由$\overrightarrow v=\overrightarrow{v_1}+\overrightarrow{v_2}=(\sqrt{3}+3,\sqrt{3}+1)$,
即$|\overrightarrow v{|^2}=16+8\sqrt{3}$
所以$|\overrightarrow v|=\sqrt{16+8\sqrt{3}}=2(\sqrt{3}+1)$
所以$cos<\overrightarrow{v_1},\overrightarrow v>=\frac{{\overrightarrow v•\overrightarrow{v_1}}}{{|\overrightarrow v||\overrightarrow{v_1}|}}=\frac{{2\sqrt{3}+6}}{{2(\sqrt{3}+1)•2}}=\frac{{\sqrt{3}}}{2}$,
即所以渡船的实际速度与水流速度的夹角$\frac{π}{6}$;
(Ⅱ)由(Ⅰ)知船垂直方向速度为$|\overrightarrow v|•sin\frac{π}{6}=\sqrt{3}+1$
所以渡船过河所需要的时间$\frac{{600(\sqrt{3}+1)}}{{\sqrt{3}+1}}=600$s.…(12分)
方法二:(正、余弦定理)
(Ⅰ)如图所示,$\overrightarrow{OA}=\overrightarrow{v_1},\overrightarrow{OB}=\overrightarrow{v_2}$,设渡船的合速度$\overrightarrow v$,则$\overrightarrow{OC}=\overrightarrow v$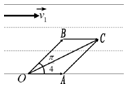
由条件$∠AOB=\frac{π}{4}$,$|\overrightarrow{OA}|=2$,$|\overrightarrow{OB}|=\sqrt{6}+\sqrt{2}$
根据向量的平行四边形法则有:$∠OAC=\frac{3π}{4}$,$|\overrightarrow{OA}|=2$,$|\overrightarrow{AC}|=\sqrt{6}+\sqrt{2}$
在△OAC中,由余弦定理得$|\overrightarrow{OC}{|^2}=|\overrightarrow{OA}{|^2}+|\overrightarrow{AC}{|^2}-2|\overrightarrow{OA}||\overrightarrow{AC}|cos∠OAC$=$4+8+2\sqrt{12}+4(\sqrt{3}+1)=\sqrt{4{{(\sqrt{3}+1)}^2}}=2(\sqrt{3}+1)$,
在△OAC中,由正弦定理得$\frac{{|\overrightarrow{AC}|}}{sin∠AOC}=\frac{{|\overrightarrow{OC}|}}{sin∠OAC}$,得$sin∠AOC=\frac{{(\sqrt{6}+\sqrt{2})\frac{{\sqrt{2}}}{2}}}{{2(\sqrt{3}+1)}}=\frac{1}{2}$
所以渡船的实际速度与水流速度的夹角$\frac{π}{6}$;
(Ⅱ)由(Ⅰ)知船所走过路程为$\frac{{600(\sqrt{3}+1)}}{sin∠AOC}=1200(\sqrt{3}+1)$
所以渡船过河所需要的时间$\frac{{1200(\sqrt{3}+1)}}{{2(\sqrt{3}+1)}}=600$s.
点评 本题考查了向量的坐标运算和向量的夹角公式,以及正弦定理和余弦定理,属于中档题

 高中必刷题系列答案
高中必刷题系列答案| A. | 0.2 | B. | 0.3 | C. | 0.7 | D. | 与σ的值有关 |
(1)“x2+2x-3<0”是命题
(2)命题“若p,则q”的否命题是“若p,则¬q”
(3)当q是p的必要条件时,p是q的充分条件
(4)“若p不成立,则q不成立”等价于“若q成立,则p成立”
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |