题目内容
16.已知函数f(x)=ax-lnax+x2(a>0,a≠1)(Ⅰ)求函数f(x)在点(0,f(0))处的切线方程
(Ⅱ)求函数f(x)单调递增区间
(Ⅲ)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1(e是自然对数的底数),求实数a的取值范围.
分析 (Ⅰ)求出函数的导数,计算f(0),f′(0),求出切线方程即可;
(Ⅱ)求出函数f(x)的导数,根据导函数的单调性判断函数f(x)的单调性即可;
(Ⅲ)问题转化为f(x)max-f(x)min≥e-1即可,通过讨论a的范围结合函数的单调性确定a的具体范围即可.
解答 解:(Ⅰ)∵函数f(x)=ax-xlna+x2,(a>0,a≠1),
∴f′(x)=axlna+2x-lna,f′(0)=0,
又∵f(0)=1,∴函数f(x)在点(0,f(0))处的切线方程是y=1;
(Ⅱ)由(Ⅰ)得:f′(x)=axlna+2x-lna=2x+(ax-1)lna,
∴f″(x)=2+ax(lna)2>0,
故a>0,a≠1时,总有f′(x)在R递增,
又f′(0)=0,∴不等式f′(x)>0的解集是(0,+∞),
故函数f(x)在(0,+∞)递增;
(Ⅲ)∵?x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1成立,
而当x∈[-1,1]时,|f(x1)-f(x2)|≤f(x)max-f(x)min,
∴只需f(x)max-f(x)min≥e-1即可,
∵x变化时,f′(x),f(x)的变化情况如下:
| x | (-∞,0) | 0 | (0,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
x∈[-1,1]时,f(x)的最小值是f(0)=1,f(x)的最大值是f(-1)或f(1),
∵f(1)-f(-1)=a-$\frac{1}{a}$-2lna,
令g(a)=a-$\frac{1}{a}$-2lna,(a>0),g′(a)=${(1-\frac{1}{a})}^{2}$>0,
∴g(a)在a∈(0,+∞)递增,而g(1)=0,
故a>1时,g(a)>0,即f(1)>f(-1),
0<a<1时,g(a)<0,即f(1)<f(-1),
∴①a>1时,f(1)-f(0)≥e-1,即a-lna≥e-1,
函数y=a-lna在(1,+∞)递增,则a≥e;
②0<a<1时,f(-1)-f(0)≥e-1,即$\frac{1}{a}$+lna≥e-1,
函数y=$\frac{1}{a}$+lna在(0,1)递减,则0<a≤$\frac{1}{e}$,
综上,a的范围是(0,$\frac{1}{e}$]∪[e,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道中档题.

练习册系列答案
相关题目
 已知渡船在静水中速度$\overrightarrow{v_2}$的大小为$(\sqrt{6}+\sqrt{2})$m/s,河水流速$\overrightarrow{v_1}$的大小为2m/s.如图渡船船头方向与水流方向成$\frac{π}{4}$夹角,且河面垂直宽度为$600(\sqrt{3}+1)m$.
已知渡船在静水中速度$\overrightarrow{v_2}$的大小为$(\sqrt{6}+\sqrt{2})$m/s,河水流速$\overrightarrow{v_1}$的大小为2m/s.如图渡船船头方向与水流方向成$\frac{π}{4}$夹角,且河面垂直宽度为$600(\sqrt{3}+1)m$.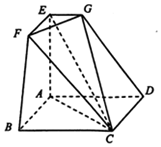 如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1,AE=3
如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1,AE=3