题目内容
12.已知函数f(x)=|lgx|,(1)判断f($\frac{1}{4}$)、f($\frac{1}{3}$)、f(2)的大小关系;
(2)若0<a<b,且f(a)>f(b),试比较ab与1的大小.
分析 (1)化简f($\frac{1}{4}$)=lg4,f($\frac{1}{3}$)=lg3,f(2)=lg2;从而利用对数函数的单调性比较大小即可;
(2)由0<a<b,且f(a)>f(b)可得0<a<b<1或0<a<1≤b,从而分类讨论比较大小.
解答 解:(1)f($\frac{1}{4}$)=|lg$\frac{1}{4}$|=lg4,
f($\frac{1}{3}$)=|lg$\frac{1}{3}$|=lg3,
f(2)=|lg2|=lg2;
故f(2)<f($\frac{1}{3}$)<f($\frac{1}{4}$);
(2)∵0<a<b,且f(a)>f(b),
∴0<a<b<1或0<a<1≤b,
①当0<a<b<1时,ab<1;
②当0<a<1≤b时,-lga>lgb,
故lgab<0,
故ab<1;
综上所述,ab<1.
点评 本题考查了学生的化简运算能力及分类讨论的思想应用.

练习册系列答案
相关题目
14.设O是△ABC的外接圆圆心,且$\overrightarrow{OA}+\sqrt{3}\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow 0$,则∠AOC=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{5π}{6}$ |
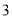 ,且每个顶点都在球
,且每个顶点都在球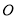 的表面上,则球
的表面上,则球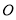 的半径为( )
的半径为( )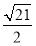 B.
B.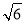 C.
C.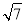 D.
D.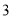
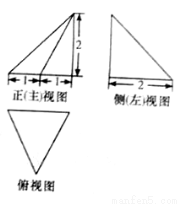
 B.
B. C.
C.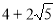 D.
D.