题目内容
8.函数f(x)=sin(πx)-$\frac{1}{x+1}$,x∈[-4,2]的所有零点之和为-4.分析 由题意函数y=sin(πx)-$\frac{1}{x+1}$,x∈[-4,2]的零点,即sin(πx)=$\frac{1}{x+1}$的根;作出函数y=sin(πx)与y=$\frac{1}{x+1}$的图象结合函数的对称性,可得答案.
解答 解:函数y=sin(πx)-$\frac{1}{x+1}$,x∈[-4,2]的零点,即sin(πx)=$\frac{1}{x+1}$的根;
作出函数y=2sin(πx)与y=$\frac{1}{x+1}$在x∈[-4,2]上的图象,如下图所示: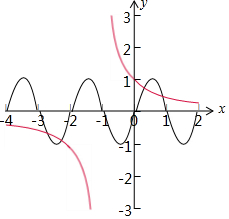
由图可得:两个函数的图象有4个不同的交点,
且两两关于点(-1,0)对称,
故四个点横坐标之和为-4,
即函数f(x)=sin(πx)-$\frac{1}{x+1}$,x∈[-4,2]的所有零点之和为-4,
故答案为:-4.
点评 本题主要考查正弦函数的图象特征,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
18.某蛋糕店每天做若干个生日蛋糕,每个制作成本为50元,当天以每个100元售出,若当天白天售不出,则当晚已30元/个价格作普通蛋糕低价售出,可以全部售完.
(1)若蛋糕店每天做20个生日蛋糕,求当天的利润y(单位:元)关于当天生日蛋糕的需求量n(单位个,n∈N*)的函数关系;
(2)蛋糕店记录了100天生日蛋糕的日需求量(单位:个)整理得下表:
(ⅰ)假设蛋糕店在这100天内每天制作20个生日蛋糕,求这100天的日利润(单位:元)的平均数;
(ⅱ)若蛋糕店一天制作20个生日蛋糕,以100天记录的各需求量的频率作为概率,求当天利润不少于900元的概率.
(1)若蛋糕店每天做20个生日蛋糕,求当天的利润y(单位:元)关于当天生日蛋糕的需求量n(单位个,n∈N*)的函数关系;
(2)蛋糕店记录了100天生日蛋糕的日需求量(单位:个)整理得下表:
| 日需求量n | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 频数(天) | 10 | 20 | 20 | 14 | 13 | 13 | 10 |
(ⅱ)若蛋糕店一天制作20个生日蛋糕,以100天记录的各需求量的频率作为概率,求当天利润不少于900元的概率.
16.设x,y满足$\left\{\begin{array}{l}{x-y≤0}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$,则(x+1)2+y2的最小值为( )
| A. | 1 | B. | $\frac{9}{2}$ | C. | 5 | D. | 9 |
20.在等差数列{an}中,a3+a4+a5+a6+a7=400,则a2+a8=( )
| A. | 40 | B. | 80 | C. | 160 | D. | 320 |
17.如图,OABC是四面体,G是△ABC的重心,G1是OG上一点,且OG=3OG1,则( )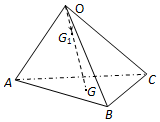

| A. | $\overrightarrow{O{G}_{1}}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G}_{1}}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{3}{4}$$\overrightarrow{OB}$+$\frac{3}{4}$$\overrightarrow{OC}$ | D. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{9}$$\overrightarrow{OA}$+$\frac{1}{9}$$\overrightarrow{OB}$+$\frac{1}{9}$$\overrightarrow{OC}$ |
18.等差数列{an}前n项和为Sn,公差d=-2,S3=21,则a1的值为( )
| A. | 10 | B. | 9 | C. | 6 | D. | 5 |