题目内容
17.如图,OABC是四面体,G是△ABC的重心,G1是OG上一点,且OG=3OG1,则( )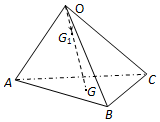
| A. | $\overrightarrow{O{G}_{1}}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G}_{1}}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{3}{4}$$\overrightarrow{OB}$+$\frac{3}{4}$$\overrightarrow{OC}$ | D. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{9}$$\overrightarrow{OA}$+$\frac{1}{9}$$\overrightarrow{OB}$+$\frac{1}{9}$$\overrightarrow{OC}$ |
分析 根据G是三角形ABC的重心,结合空间向量的线性运算法则,即可得出结果.
解答 解:∵G是△ABC的重心,
∴$\overrightarrow{AG}$=$\frac{2}{3}$×$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴$\overrightarrow{OG}$=$\overrightarrow{OA}$+$\overrightarrow{AG}$
=$\overrightarrow{OA}$+$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)
=$\overrightarrow{OA}$+$\frac{1}{3}$($\overrightarrow{OB}$-$\overrightarrow{OA}$+$\overrightarrow{OC}$-$\overrightarrow{OA}$)
=$\frac{1}{3}$($\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$)
$\overrightarrow{OG}$=3$\overrightarrow{{OG}_{1}}$
∴$\overrightarrow{{OG}_{1}}$=$\frac{1}{3}$$\overrightarrow{OG}$=$\frac{1}{9}$($\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$)=$\frac{1}{9}$$\overrightarrow{OA}$+$\frac{1}{9}$$\overrightarrow{OB}$+$\frac{1}{9}$$\overrightarrow{OC}$.
故选:D.
点评 本题考查了三角形重心的应用以及空间向量的化简与运算问题,是基础题目.

 名师点拨卷系列答案
名师点拨卷系列答案| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| 气温(°C) | 20 | 16 | 12 | 4 |
| 用电量(度) | 14 | 28 | 44 | 62 |
| A. | 70 | B. | 68 | C. | 64 | D. | 62 |
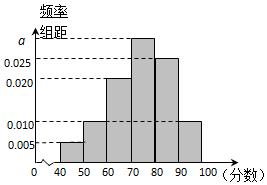 某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.