题目内容
15.若直线l1:ax+2y+6=0与直线l2:x+(a-1)y-1=0垂直,则实数a=( )| A. | $\frac{2}{3}$ | B. | -1 | C. | 2 | D. | -1或2 |
分析 由直线的垂直关系可得a•1+2(a-1)=0,解方程可得.
解答 解:∵直线l1:ax+2y+6=0与直线l2:x+(a-1)y-1=0垂直,
∴a•1+2(a-1)=0,解得a=$\frac{2}{3}$,
故选:A.
点评 本题考查直线的一般式方程和垂直关系,属基础题.

练习册系列答案
相关题目
5.已知集合A={x|1≤x≤3},B={x|0<x<a},若A⊆B,则实数a的范围是( )
| A. | [3,+∞) | B. | (3,+∞) | C. | [-∞,3] | D. | [-∞,3) |
10.已知圆M:(x+$\sqrt{7}$)2+y2=64,定点N($\sqrt{7}$,0),点P为圆M上的动点,点Q在NP上,点G 在线段MP上,且满足$\overrightarrow{NP}$=2$\overrightarrow{NQ}$,$\overrightarrow{GQ}$•$\overrightarrow{NP}$=0,则点G的轨迹方程是( )
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{64}+\frac{y^2}{57}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{57}=1$ |
20.已知两定点A(-3,0),B(3,0),如果动点P满足|PA|=2|PB|,则点P的轨迹所包围的图形的面积等于( )
| A. | π | B. | 4π | C. | 9π | D. | 16π |
7.等比数列{an}中,S2=2,S4=8,则S6=( )
| A. | -32 | B. | 32 | C. | -26 | D. | 26 |
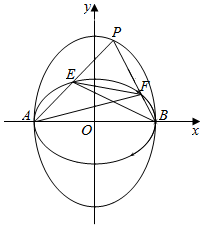 椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.
椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.