题目内容
16.设f(x)=$\left\{\begin{array}{l}{x-2,(x≥10)}\\{f[f(x+6)],(x<10)}\end{array}\right.$,则f(4)的值为( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
分析 直接利用分段函数,化简求解函数值即可.
解答 解:f(x)=$\left\{\begin{array}{l}{x-2,(x≥10)}\\{f[f(x+6)],(x<10)}\end{array}\right.$,
则f(4)=f[f(4+6)]=f(10-2)=f(8)=f[f(8+6)]=f(f(14))=f(12)=12-2=10.
故选:A.
点评 本题考查分段函数的应用,函数值的求法,考查计算能力.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
4.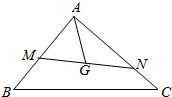 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{{3+2\sqrt{2}}}{3}$ | D. | $\frac{3}{4}$ |
11.角-420°终边上有一异于原点的点(4,-a),则a的值是( )
| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | ±4$\sqrt{3}$ | D. | $\sqrt{3}$ |
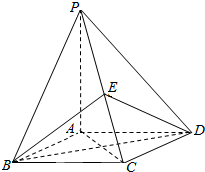 如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.
如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.