题目内容
下列四组函数中,表示相等函数的一组是( )
| A、y=2log2x与y=log2x2 | |||
B、y=±x与y=
| |||
C、y=x与y=
| |||
D、y=|x|与y=(
|
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:根据两个函数的定义域相同,对应关系也相同,这样的函数是相等函数,进行判断即可.
解答:
解:A、函数y=2log2x的定义域满足x>0,函数y=log2x2的定义域满足x≠0,不是相等函数,A错误;
B、函数y=±x,值域为R,函数y=
=|x|,值域满足y≥0,不是相等函数,B错误;
C、y=x(x∈R)与y=
=x(x∈R)的定义域相同,对应关系也相同,是相等函数;
D、函数y=|x|的定义域为R,函数y=(
)2的定义域满足x≥0,不是相等函数,D错误;
故选:C
B、函数y=±x,值域为R,函数y=
| x2 |
C、y=x(x∈R)与y=
| 3 | x3 |
D、函数y=|x|的定义域为R,函数y=(
| x |
故选:C
点评:本题考查了判断两个函数是否为同一函数的问题,解题时应判断它们的定义域是否相同,对应关系是否也相同.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知正方形AP1P2P3的边长为4,点B,C分别是边P1P2,P2P3的中点,沿AB,BC,CA折叠成一个三棱锥P-ABC(使P1,P2,P3重合于点P),则三棱锥P-ABC的外接球的体积为( )
| A、24π | ||
B、8
| ||
C、4
| ||
| D、4π |
已知正方形ABCD的边长为2,E为CD的中点,F为AD的中点,则
•
=( )
| AE |
| BF |
| A、0 | B、1 | C、2 | D、4 |
小红拿着一物体的三视图(如图所示)给小明看,并让小明猜想这个物件的形状是( )


| A、长方形 | B、圆柱 |
| C、立方体 | D、圆锥 |
函数f(x)=2sin(2x+
)在区间(-π,π)上零点的个数为( )
| π |
| 3 |
| A、5 | B、4 | C、3 | D、2 |
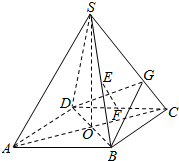 正四棱锥S-ABCD中,O为底面中心,SO=AB=2,E、F分别为SB、CD的中点.
正四棱锥S-ABCD中,O为底面中心,SO=AB=2,E、F分别为SB、CD的中点.