题目内容
圆心在y轴上且过点（3，1）的圆与x轴相切，则该圆的方程是 ．
考点：圆的标准方程
专题：直线与圆
分析：由题意求出圆的圆心与半径，即可写出圆的方程．
解答：
解：圆心在y轴上且过点（3，1）的圆与x轴相切，
设圆的圆心（0，r），半径为r．
则：
=r．
解得r=5．
所求圆的方程为：x2+（y-5）2=25．
故答案为：x2+（y-5）2=25．
设圆的圆心（0，r），半径为r．
则：
| (3-o)2+(1-r)2 |
解得r=5．
所求圆的方程为：x2+（y-5）2=25．
故答案为：x2+（y-5）2=25．
点评：本题考查圆的方程的求法，求出圆的圆心与半径是解题的关键．
练习册系列答案
相关题目
设变量x，y满足
，则
的取值范围是（ ）
|
| y-2 |
| x+1 |
A、（-∞，-
| ||
B、[-3，
| ||
C、[-
| ||
D、（-∞，-3]∪[
|
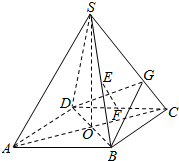正四棱锥S-ABCD中，O为底面中心，SO=AB=2，E、F分别为SB、CD的中点．