题目内容
 如图,几何体EF-ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.
如图,几何体EF-ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.(1)求证:AC⊥FB
(2)求二面角E-FB-C的大小.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)由题意得,AD⊥DC,AD⊥DF,从而AD⊥FC,DC⊥FC,由此能证明AC⊥FB.
(2)以D为原点,DA,DC,DE所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角E-FB-C的大小.
(2)以D为原点,DA,DC,DE所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角E-FB-C的大小.
解答:
 解:(1)证明:由题意得,AD⊥DC,AD⊥DF,且DC∩DF=D,
解:(1)证明:由题意得,AD⊥DC,AD⊥DF,且DC∩DF=D,
∴AD⊥平面CDEF,∴AD⊥FC,…(2分)
∵四边形CDEF为正方形.∴DC⊥FC
由DC∩AD=D∴FC⊥平面ABCD,∴FC⊥AC…(4分)
又∵四边形ABCD为直角梯形,
AB∥CD,AD⊥DC,AD=2,AB=4
∴AC=2
,BC=2
,则有AC2+BC2=AB2
∴AC⊥BC
由BC∩FC=C,∴AC⊥平面FCB,∴AC⊥FB.…(6分)
(2)解:由(1)知AD,DC,DE所在直线相互垂直,
故以D为原点,DA,DC,DE所在直线分别为x,y,z轴,
建立如图所示的空间直角坐标系,…(7分)
可得D(0,0,0),F(0,2,2),B(2,4,0),
E(0,0,2),C(0,2,0),A(2,0,0),
由(1)知平面FCB的法向量为
=(-2,2,0),
∴
=(0,2,0),
=(2,2,-2),…(8分)
设平面EFB的法向量为
=(x,y,z),
则有:
⇒
⇒
令z=1则
=(1,0,1),…(10分)
设二面角E-FB-C的大小为θ,
cosθ=
=
=-
,
∵θ∈(0,π),∴θ=
.…(12分)
 解:(1)证明:由题意得,AD⊥DC,AD⊥DF,且DC∩DF=D,
解:(1)证明:由题意得,AD⊥DC,AD⊥DF,且DC∩DF=D,∴AD⊥平面CDEF,∴AD⊥FC,…(2分)
∵四边形CDEF为正方形.∴DC⊥FC
由DC∩AD=D∴FC⊥平面ABCD,∴FC⊥AC…(4分)
又∵四边形ABCD为直角梯形,
AB∥CD,AD⊥DC,AD=2,AB=4
∴AC=2
| 2 |
| 2 |
∴AC⊥BC
由BC∩FC=C,∴AC⊥平面FCB,∴AC⊥FB.…(6分)
(2)解:由(1)知AD,DC,DE所在直线相互垂直,
故以D为原点,DA,DC,DE所在直线分别为x,y,z轴,
建立如图所示的空间直角坐标系,…(7分)
可得D(0,0,0),F(0,2,2),B(2,4,0),
E(0,0,2),C(0,2,0),A(2,0,0),
由(1)知平面FCB的法向量为
| AC |
∴
| EF |
| FB |
设平面EFB的法向量为
| n |
则有:
|
|
|
令z=1则
| n |
设二面角E-FB-C的大小为θ,
cosθ=
| ||||
|
|
| 1×(-2)+2×0+0×1 | ||||
|
| 1 |
| 2 |
∵θ∈(0,π),∴θ=
| π |
| 3 |
点评:本题考查异面直线垂直的证明,考查二面角的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
设变量x,y满足
,则
的取值范围是( )
|
| y-2 |
| x+1 |
A、(-∞,-
| ||
B、[-3,
| ||
C、[-
| ||
D、(-∞,-3]∪[
|
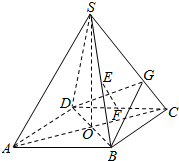 正四棱锥S-ABCD中,O为底面中心,SO=AB=2,E、F分别为SB、CD的中点.
正四棱锥S-ABCD中,O为底面中心,SO=AB=2,E、F分别为SB、CD的中点.