题目内容
已知函数f(x)=alnx+
bx2-(a+b)x,
(1)当a=1,b=0时,求f(x)的最大值;
(2)当b=1时,设α,β是f(x)的两个极值点,且α<β,β∈(1,e](其中e为自然对数的底数).求证:对任意的x1,x2∈[α,β],|f(x1)-f(x2)|<1.
| 1 |
| 2 |
(1)当a=1,b=0时,求f(x)的最大值;
(2)当b=1时,设α,β是f(x)的两个极值点,且α<β,β∈(1,e](其中e为自然对数的底数).求证:对任意的x1,x2∈[α,β],|f(x1)-f(x2)|<1.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题:导数的综合应用
分析:本题(1)在条件a=1,b=0下,对函数f(x)求导函数,根据导函数值正负,得到函数的单调区间,求出f(x)的最大值,得到本题结论;(2)先根据条件α,β是f(x)的两个极值点,得到α,β是f′(x)=0的两个根,将|f(x1)-f(x2)|转化为[f(x)]max、[f(x)]min的关系得到关于a的函数,再构造新函数,求出最值,得到本题结论.
解答:
解:(1)∵函数f(x)=alnx+
bx2-(a+b)x,
∴x>0,f′(x)=
+bx-(a+b),
(1)当a=1,b=0时,f′(x)=
,
令f′(x)>0,得:0<x<1,
令f′(x)<0,得:x>1.
∴函数f(x)在区间(0,1)上单调递增;在(1,+∞)上单调递减,
∴[f(x)]max=f(1)=-1.
(2)当b=1时,f(x)=alnx+
x2-(a+1)x,
则f′(x)=
,
令f′(x)=0,得:x=1或x=a.
∵α,β是f(x)的两个极值点,且α<β,β∈(1,e],
∴α=1,β=a∈(1,e],
∴当x∈[α,β]时,f′(x)≤0,即f(x)在[α,β]上单调递减,
∴[f(x)]min=f(a),[f(x)]max=f(1),
∴|f(x1)-f(x2)|≤[f(x)]max-[f(x)]min=f(1)-f(a)=
a2-alna-
.
令g(a))=
a2-alna-
.
则g′(a)=a-1-lna,
由(1)知:lnx-x≤-1,即lnx≤x-1,
即g′(a)≥0,g(a)在(1,e]单调递增,
∴g(a)≤g(e)=
e2-e-
=e(
e-1)-
<3(
-1)-
=1.
∴|f(x1)-f(x2)|<1.
| 1 |
| 2 |
∴x>0,f′(x)=
| a |
| x |
(1)当a=1,b=0时,f′(x)=
| 1-x |
| x |
令f′(x)>0,得:0<x<1,
令f′(x)<0,得:x>1.
∴函数f(x)在区间(0,1)上单调递增;在(1,+∞)上单调递减,
∴[f(x)]max=f(1)=-1.
(2)当b=1时,f(x)=alnx+
| 1 |
| 2 |
则f′(x)=
| (x-1)(x-a) |
| x |
令f′(x)=0,得:x=1或x=a.
∵α,β是f(x)的两个极值点,且α<β,β∈(1,e],
∴α=1,β=a∈(1,e],
∴当x∈[α,β]时,f′(x)≤0,即f(x)在[α,β]上单调递减,
∴[f(x)]min=f(a),[f(x)]max=f(1),
∴|f(x1)-f(x2)|≤[f(x)]max-[f(x)]min=f(1)-f(a)=
| 1 |
| 2 |
| 1 |
| 2 |
令g(a))=
| 1 |
| 2 |
| 1 |
| 2 |
则g′(a)=a-1-lna,
由(1)知:lnx-x≤-1,即lnx≤x-1,
即g′(a)≥0,g(a)在(1,e]单调递增,
∴g(a)≤g(e)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴|f(x1)-f(x2)|<1.
点评:本题考查了导函数在函数研究中的应用,还考查了构造函数的思想,本题思维难度较大,计算复杂,属于难题.

练习册系列答案
相关题目
设a,b∈R,则“a≥1且“b≥1”是“a+b≥2”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
若直线y=x+b与曲线x=
恰有一个公共点,则b的取值范围是( )
| 1-y2 |
| A、-1<b≤1 | ||
| B、-1≤b≤1 | ||
C、-
| ||
D、-1<b≤1或b=-
|
用秦九韶算法计算函数f(x)=12+35x-8x2+79x3+6x4+5x5+3x6当x=-4时的函数值时.v2的值为( )
| A、3 | B、-7 | C、34 | D、-57 |
设等差数列{an}满足:
=1,公差d∈(-1,0).若当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则首项a1的取值范围是( )
| sin2a3-cos2a3+cos2a3cos2a6-sin2a3sin2a6 |
| sin(a4+a5) |
A、[
| ||||
B、[
| ||||
C、(
| ||||
D、(
|
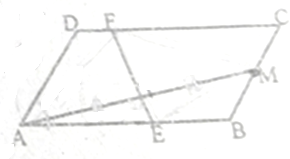 已知,平行四边形ABCD中,AB=4,AD=2
已知,平行四边形ABCD中,AB=4,AD=2