题目内容
16．化简$\sqrt{1-si{n}^{2}α}$的结果为（ ）| A． | sinα | B． | -sinα | C． | ±cosα | D． | -cosα |
分析 由已知利用同角三角函数基本关系式即可计算得解．
解答 解：$\sqrt{1-si{n}^{2}α}$=$\sqrt{co{s}^{2}α}$=±cosα．
故选：C．
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用，属于基础题．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
10．若角α的始边是x轴正半轴，终边过点P（4，-3），则cosα的值是（ ）
| A． | 4 | B． | -3 | C． | $\frac{4}{5}$ | D． | -$\frac{3}{5}$ |
11．已知cos（$\frac{5π}{12}$-θ）=$\frac{1}{3}$，则sin（$\frac{π}{12}$+θ）的值是（ ）
| A． | -$\frac{1}{3}$ | B． | -$\frac{2\sqrt{2}}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |
1．函数f（x）=ax3+6x2+（a-1）x-5有极值的充要条件是（ ）
| A． | a=-3或a=4 | B． | -3＜a＜4 | C． | a＞4或a＜-3 | D． | a∈R |
如图：空间四边形ABCD中，E，F，G，H分别是AB，AD，CD，CB上的点，且EF∥GH，求证：EF∥BD．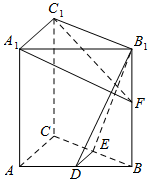
如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1．求证：