题目内容
15.设实数x1、x2是函数$f(x)=|{lnx}|-{({\frac{1}{2}})^x}$的两个零点,则( )| A. | x1x2<0 | B. | 0<x1x2<1 | C. | x1x2=1 | D. | x1x2>1 |
分析 能够分析出f(x)的零点便是函数y=|lnx|和函数y=($\frac{1}{2}$)x交点的横坐标,从而可画出这两个函数图象,由图象懒虫不等式组,然后求解即可.
解答 解:令f(x)=0,∴|lnx|=($\frac{1}{2}$)x;
∴函数f(x)的零点便是上面方程的解,即是函数y=|lnx|和函数y=($\frac{1}{2}$)x的交点,
画出这两个函数图象如下: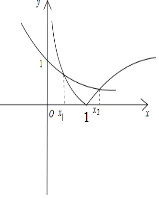
由图看出$\frac{1}{2}$<-lnx1<1,-1<lnx1<0,0<lnx2<$\frac{1}{2}$;
∴-1<lnx1+lnx2<0;
∴-1<lnx1x2<0;
∴0<$\frac{1}{e}$<x1x2<1
故选:B.
点评 考查函数零点的概念,函数零点和方程解的关系,方程f(x)=g(x)的解和函数f(x)与g(x)交点的关系,对数的运算,以及对数函数的单调性.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
5.在等差数列{an}中,a1=-6,公差为d,前n项和为Sn,当且仅当n=6时,Sn取得最小值,则d的取值范围为( )
| A. | $(-1,-\frac{7}{8})$ | B. | (0,+∞) | C. | (-∞,0) | D. | $(1,\frac{6}{5})$ |
10.若角α的始边是x轴正半轴,终边过点P(4,-3),则cosα的值是( )
| A. | 4 | B. | -3 | C. | $\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
1.函数f(x)=ax3+6x2+(a-1)x-5有极值的充要条件是( )
| A. | a=-3或a=4 | B. | -3<a<4 | C. | a>4或a<-3 | D. | a∈R |
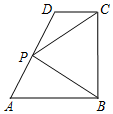 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x).
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x). 如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点
如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点