题目内容
函数f（x）=
（x＞0）的值域为（ ）
| 2x-1 |
| x+1 |
| A、（-∞，2） |
| B、（-∞，2）∪（2，+∞） |
| C、[-1，2] |
| D、（-1，2） |
考点：函数的值域
专题：计算题,函数的性质及应用
分析：分离常数法，化f（x）=
=2-
求函数的值域．
| 2x-1 |
| x+1 |
| 3 |
| x+1 |
解答：
解：f（x）=
=2-
，
∵x＞0，∴0＜
＜3，
∴-1＜2-
＜2，
故函数的值域为：（-1，2）．
故选D．
| 2x-1 |
| x+1 |
| 3 |
| x+1 |
∵x＞0，∴0＜
| 3 |
| x+1 |
∴-1＜2-
| 3 |
| x+1 |
故函数的值域为：（-1，2）．
故选D．
点评：本题考查了函数值域的求法．高中函数值域求法有：1、观察法，2、配方法，3、反函数法，4、判别式法；5、换元法，6、数形结合法，7、不等式法，8、分离常数法，9、单调性法，10、利用导数求函数的值域，11、最值法，12、构造法，13、比例法．要根据题意选择．
练习册系列答案
阅读快车系列答案
相关题目
已知x，y满足
，则x2+y2的最大值为（ ）
|
| A、5 | B、9 | C、16 | D、25 |
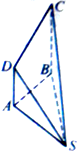如图，在四棱锥S-ABCD中，DA⊥平面SAB，BC⊥平面SAB，AB=BC=SA=2AD=2，∠BAS=120°．