题目内容
x≠1或y≠2是x+y≠3的 条件.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的性质,利用充分条件和必要条件的定义进行判断即可得到结论.
解答:
解:根据逆否命题的等价性,只需要判断x+y=3与x=1且y=2的条件关系即可.
若x=0,y=3时,满足x+y=3,但此时x=1且y=2,不成立,即充分性不成立.
若x=1,y=2时,则x+y=3成立,即必要性成立.
即x+y=3是x=1且y=2的必要不充分条件,
即“x≠1或y≠2”是“x+y≠3”的必要不充分条件,
故答案为:必要非充分
若x=0,y=3时,满足x+y=3,但此时x=1且y=2,不成立,即充分性不成立.
若x=1,y=2时,则x+y=3成立,即必要性成立.
即x+y=3是x=1且y=2的必要不充分条件,
即“x≠1或y≠2”是“x+y≠3”的必要不充分条件,
故答案为:必要非充分
点评:判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
函数y=cos(2x-
)的图象的一条对称轴方程是( )
| π |
| 2 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
| D、x=π |
计算:2i÷(1+i)等于( )
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积为( )
| A、9 | ||
| B、18 | ||
C、9
| ||
D、18
|
若函数f(x+1)的定义域是[-1,1],则函数g(x)=
的定义域是( )
| f(2x) |
| x-1 |
| A、[-1,0] |
| B、[0,1) |
| C、[0,1)∪(1.4] |
| D、(0,1) |
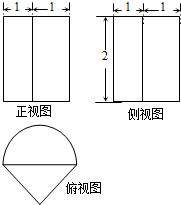 如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )
如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )A、2+3π+4
| ||
B、2+2π+4
| ||
C、8+5π+2
| ||
D、6+3π+2
|