题目内容
设f(x)是(-∞,+∞)上的奇函数,且f(x+2)=-f (x),当0≤x≤1时,f(x)=x.
(1)求f(3)的值;
(2)当-4≤x≤4时,求f(x)的图象与x轴围成图形的面积.
(1)求f(3)的值;
(2)当-4≤x≤4时,求f(x)的图象与x轴围成图形的面积.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)由已知的等式f(x+2)=-f (x)结合函数的奇偶性求得函数的周期,把f(3)转化为f(1)结合当0≤x≤1时,f(x)=x求得f(3)的值;
(2)由已知等式求得函数的对称轴方程,结合(1)进一步得到函数的图象,再由三角形的面积公式求得f(x)的图象与x轴围成图形的面积.
(2)由已知等式求得函数的对称轴方程,结合(1)进一步得到函数的图象,再由三角形的面积公式求得f(x)的图象与x轴围成图形的面积.
解答:
解:(1)∵f(x)是(-∞,+∞)上的奇函数,且f(x+2)=-f (x),
则f(x+2+2)=-f (x+2)=-[-f(x)]=f(x),
∴f(x)的周期为4.
∴f(3)=f(-4+3)=f(-1)=-f(1).
∵0≤x≤1时,f(x)=x,
∴f(3)=-f(1)=-1;
(2)由f(x+2)=-f (x),得f(x+2)=f(-x).
∴函数f(x)的对称轴方程为x=1.
结合(1)可知,f(x)的图象如图:
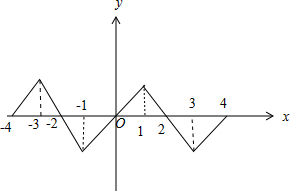
∴当-4≤x≤4时,f(x)的图象与x轴围成图形的面积为4×
×2×1=4.
则f(x+2+2)=-f (x+2)=-[-f(x)]=f(x),
∴f(x)的周期为4.
∴f(3)=f(-4+3)=f(-1)=-f(1).
∵0≤x≤1时,f(x)=x,
∴f(3)=-f(1)=-1;
(2)由f(x+2)=-f (x),得f(x+2)=f(-x).
∴函数f(x)的对称轴方程为x=1.
结合(1)可知,f(x)的图象如图:

∴当-4≤x≤4时,f(x)的图象与x轴围成图形的面积为4×
| 1 |
| 2 |
点评:本题考查了函数的周期性、奇偶性的性质,考查了函数对称轴方程的求法,是中档题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
复数z在复平面内的对应点为(-1,1),
是z的共轭复数,则
+|z|=( )
. |
| z |
| 2 |
. |
| z |
A、
| ||
B、-
| ||
C、
| ||
D、
|
棱长为a的正方体ABCD-A1B1C1D1中,E、F、G分别是AB、BC,BB1的中点;过点E、F、G作截面,截去正方形一角,则剩下部分的体积是( )
| A、a3 | ||
B、
| ||
C、
| ||
D、
|
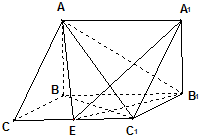 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已BC=1,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已BC=1,∠BCC1=