Question

已知三棱锥S-ABC的所有顶点都在球O的球面上，SA⊥平面ABC，AB⊥BC且AB=BC=1，SA=

2

，则球O的表面积是（　　）

• A、4π
• B、

  3

  4

  π
• C、3π
• D、

  4

  3

  π

Answer 1

考点：球的体积和表面积

专题：计算题,空间位置关系与距离,球

分析：由三棱锥S-ABC的所有顶点都在球O的球面上，SA⊥平面ABC，AB⊥BC，可得SA⊥AC，SB⊥BC，则SC的中点为球心，由勾股定理解得SC，再由球的表面积公式计算即可得到．

解答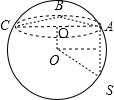： 解：如图，三棱锥S-ABC的所有顶点都在球O的球面上，
∵SA⊥平面ABC，SA=

2

，AB⊥BC且AB=BC=1，
∴AC=

1+1

=

2

，
∴SA⊥AC，SB⊥BC，
SC=

AC2+SA2

=

2+2

=2，
∴球O的半径R=

1

2

SC=1，
∴球O的表面积S=4πR²=4π．
故选A．

点评：本题考查球的表面积的求法，合理地作出图形，确定球心，求出球半径，是解题的关键．