题目内容
已知点A、B是抛物线y2=4x上的两点,O是坐标原点,
•
=0,直线AB交x轴于点C,则|
|= .
| OA |
| OB |
| OC |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:设出A,B的坐标,讨论直线斜率存在时,联立直线方程与抛物线方程,利用消元法得到关于x的一元二次方程,由
•
=0,得x1x2+y1y2=0,建立关于参数k,b的关系,消去b可得直线恒过(4,0),可得C的坐标,即可得到向量OC的模,再考虑斜率不存在,同样可得C的坐标和向量OC的模.
| OA |
| OB |
解答:
解:设点A,B的坐标分别为(x1,y1),(x2,y2)
(1)当直线l存在斜率时,设直线方程为y=kx+b,显然k≠0且b≠0.
联立方程得:
,消去y得k2x2+(2kb-4)x+b2=0
则x1x2=
,
由y12=4x1,y22=4x2,
则y1y2=4•
,
又
•
=0,则x1x2+y1y2=0,
即
+
=0,
解得b=0(舍去)或b=-4k,
故直线l的方程为:y=kx-k=k(x-4),故直线过定点(4,0),
则有C(4,0),则|
|=4.
(2)当直线l斜率不存在时,设它的方程为x=m,显然m>0,
联立方程得:
解得 y=±2
,即y1y2=-4m
又因为
•
=0,所以可得x1x2+y1y2=0,即m2-4m=0,
解得m=0(舍去)或m=4
可知直线l方程为:x=4,
故直线过定点(4,0).
即有C(4,0),则|
|=4.
故答案为:4.
(1)当直线l存在斜率时,设直线方程为y=kx+b,显然k≠0且b≠0.
联立方程得:
|
则x1x2=
| b2 |
| k2 |
由y12=4x1,y22=4x2,
则y1y2=4•
| b |
| k |
又
| OA |
| OB |
即
| b2 |
| k2 |
| 4b |
| k |
解得b=0(舍去)或b=-4k,
故直线l的方程为:y=kx-k=k(x-4),故直线过定点(4,0),
则有C(4,0),则|
| OC |
(2)当直线l斜率不存在时,设它的方程为x=m,显然m>0,
联立方程得:
|
| m |
又因为
| OA |
| OB |
解得m=0(舍去)或m=4
可知直线l方程为:x=4,
故直线过定点(4,0).
即有C(4,0),则|
| OC |
故答案为:4.
点评:本题考查向量垂直的条件,同时考查直线与抛物线的位置关系,以及证明直线恒过定点,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,其中a∈R,若对任意的非零的实数x1,存在唯一的非零的实数x2(x2≠x1),使得f(x2)=f(x1)成立,则k的最大值为( )
|
| A、-1 | B、-2 | C、-4 | D、-3 |
若关于x的方程2x=a2有负实数根,则实数a的取值范围是( )
| A、(-1,1) |
| B、(-∞,0)∪(0,+∞) |
| C、(-1,0)∪(0,1) |
| D、(-∞,-1)∪(1,+∞) |
 已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,AB⊥BC且AB=BC=1,SA=
已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,AB⊥BC且AB=BC=1,SA=| 2 |
| A、4π | ||
B、
| ||
| C、3π | ||
D、
|
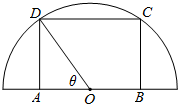 如图,在半径为10
如图,在半径为10 某公司生产部门调研发现,该公司第二、三季度的用电量与月份线性相关,数据统计如表:
某公司生产部门调研发现,该公司第二、三季度的用电量与月份线性相关,数据统计如表:
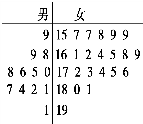 某学校举行元旦晚会,组委会招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm)身高175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.
某学校举行元旦晚会,组委会招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm)身高175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.