题目内容
用边长为1的小正方形搭如下的塔状图形,请你根据图形所反映的规律解答下列问题:
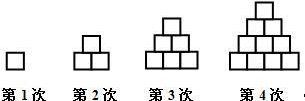
(1)填写下表:
(2)第n个图形的周长是 (用含n的代数式表示)
(3)如果第m个图形的周长恰好等于2020,请求出m的值.

(1)填写下表:
| 图形序号 | 1 | 2 | 3 | 4 | 5 | … |
| 所搭图形的周长 | 4 | 8 | 12 | … |
(3)如果第m个图形的周长恰好等于2020,请求出m的值.
考点:归纳推理
专题:计算题,推理和证明
分析:(1)第4个图形的周长是16,第5个图形的周长是20;
(2)抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论;
(3)利用(2)的结论,建立方程,即可得出结论.
(2)抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论;
(3)利用(2)的结论,建立方程,即可得出结论.
解答:
解:(1)第4个图形的周长是16,第5个图形的周长是20;
(2)由题意,第一次:1个小正方形的时候,周长等于1个正方形的周长,是1×4=4;
第二次:3个小正方形的时候,一共有4条边被遮挡,相当于少了1个小正方形的周长,所搭图形的周长为2个小正方形的周长,是2×4=8;
第三次:6个小正方形的时候,一共有13条边被遮挡,相当于少了3个小正方形的周长,所搭图形的周长为3个小正方形的周长,是3×4=12;
….
找到规律,
第n次:第几次搭建的图形的周长就相当于几个小正方形的周长是4n;
(3)4m=2020,∴m=505.
故答案为:(1)16,20;(2)4n
| 图形序号 | 1 | 2 | 3 | 4 | 5 | … |
| 所搭图形的周长 | 4 | 8 | 12 | 16 | 20 | … |
第二次:3个小正方形的时候,一共有4条边被遮挡,相当于少了1个小正方形的周长,所搭图形的周长为2个小正方形的周长,是2×4=8;
第三次:6个小正方形的时候,一共有13条边被遮挡,相当于少了3个小正方形的周长,所搭图形的周长为3个小正方形的周长,是3×4=12;
….
找到规律,
第n次:第几次搭建的图形的周长就相当于几个小正方形的周长是4n;
(3)4m=2020,∴m=505.
故答案为:(1)16,20;(2)4n
点评:本题考查归纳推理,考查学生的观察能力和空间想象能力.

练习册系列答案
相关题目
已知△ABC是等腰三角形,∠ABC=120°,以A,B为焦点的双曲线过点C,则双曲线的离心率为( )
A、1+
| ||||
B、1+
| ||||
C、
| ||||
D、
|
若关于x的方程2x=a2有负实数根,则实数a的取值范围是( )
| A、(-1,1) |
| B、(-∞,0)∪(0,+∞) |
| C、(-1,0)∪(0,1) |
| D、(-∞,-1)∪(1,+∞) |
已知曲线x2+y+1=0与双曲线x2-
=1(b>0)的渐近线相切,则此双曲线的焦距等于( )
| y2 |
| b2 |
A、2
| ||
B、2
| ||
| C、4 | ||
D、2
|
 已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,AB⊥BC且AB=BC=1,SA=
已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,AB⊥BC且AB=BC=1,SA=| 2 |
| A、4π | ||
B、
| ||
| C、3π | ||
D、
|
公比为
的等比数列{an}的各项都是正数,且a4a6=16,则a7=( )
| 1 |
| 2 |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
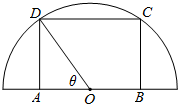 如图,在半径为10
如图,在半径为10