题目内容
已知和式S=
,当n趋向于∞时,S无限趋向于一个常数A,则A可用定积分表示为( )
| 12+22+32+…+n2 |
| n3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:定积分
专题:导数的概念及应用
分析:利用定积分的定义即可选出.
解答:
解:∵S=
=
=
×(2+
+
),
∴
=
×(2+
+
)=
.
∵
x2dx=
x3
=
,
故选:B.
| 12+22+32+…+n2 |
| n3 |
| 1 |
| n3 |
| n(n+1)(2n+1) |
| 6 |
| 1 |
| 6 |
| 3 |
| n |
| 1 |
| n2 |
∴
| lim |
| n→∞ |
| 12+22+32+…+n2 |
| n3 |
| lim |
| n→∞ |
| 1 |
| 6 |
| 3 |
| n |
| 1 |
| n2 |
| 1 |
| 3 |
∵
| ∫ | 1 0 |
| 1 |
| 3 |
| | | 1 0 |
| 1 |
| 3 |
故选:B.
点评:本题主要考查了定积分的意义,正确理解定积分的定义是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
从1,2,3,…,20这20个正整数中,每次取3个不同的数组成等比数列,则不同等比数列的个数共有( )
| A、10 | B、16 | C、20 | D、22 |
从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,则这个数能被3整除的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
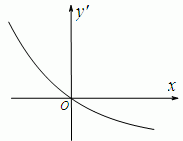 已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)=
已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)= 若aij表示n×n阶矩阵,如图所示中第i行、第j列的元素(i、j=1,2,3,…,n),其中若aij=321,则i+j=
若aij表示n×n阶矩阵,如图所示中第i行、第j列的元素(i、j=1,2,3,…,n),其中若aij=321,则i+j=