题目内容
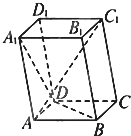已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为1的正方形．AA1=2，∠A1AB=∠A1AD=120°．（1）求线段AC1的长；
（2）求异面直线AC1与A1D所成角的余弦值．
考点：异面直线及其所成的角,点、线、面间的距离计算
专题：空间角
分析：（1）设
=
，
=
，
=
，由于
=
+
+
，利用数量积运算性质
2=(
+
+
)2=
2+
2+
2+2
•
+2
•
+2
•
即可得出．
（2）利用向量夹角公式cos＜
，
＞=
即可得出．
| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| AC1 |
| a |
| b |
| c |
| AC1 |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
（2）利用向量夹角公式cos＜
| A1D |
| AC1 |
| ||||
|
|
解答：
解：（1）设
=
，
=
，
=
，
则|
|=|
|=1，|
|=2，
•
=0，
•
=
•
=2×1×cos120°=-1．
∵
=
+
+
，
∴
2=(
+
+
)2=
2+
2+
2+2
•
+2
•
+2
•
=1+1+4+0-2-2=2，
∴|
|=
．
（2）
=
-
，
∴|
|=
=
=
．
•
=(
-
)•(
+
+
)=
•
+
2-
•
-
2=0+1-（-1）-22=-2．
∴cos＜
，
＞=
=
=-
．
∴异面直线AC1与A1D所成角的余弦值为
．
| AB |
| a |
| AD |
| b |
| AA1 |
| c |
则|
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
∵
| AC1 |
| a |
| b |
| c |
∴
| AC1 |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
∴|
| AC1 |
| 2 |
（2）
| A1D |
| b |
| c |
∴|
| A1D |
|
| 1+22-2×(-1) |
| 7 |
| A1D |
| AC1 |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| b |
| a |
| c |
| c |
∴cos＜
| A1D |
| AC1 |
| ||||
|
|
| -2 | ||||
|
| ||
| 7 |
∴异面直线AC1与A1D所成角的余弦值为
| ||
| 7 |
点评：本题考查了向量的平行六面体法则、数量积运算性质、向量夹角公式，考查了空间想象能力，考查了计算能力，属于中档题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目