题目内容
18.已知O为坐标原点,F1、F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点,A为C的左顶点,P为C上一点,且PF1⊥x轴,过点A的直线l与线段PF1交于点M,与y轴交于点E,若直线F2M与y轴交点为N,OE=2ON,则C的离心率为( )| A. | $\frac{1}{3}$ | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 根据条件求出直线AE的方程,求出N,E的坐标,利用|OE|=2|ON|的关系建立方程进行求解即可.
解答 解:∵PF1⊥x轴,∴设M(-c,t),
则A(-a,0),B(a,0),
AE的斜率k=$\frac{t}{a-c}$,则AE的方程为y=$\frac{t}{a-c}$(x+a),
令x=0,则y=$\frac{ta}{a-c}$,即E(0,$\frac{ta}{a-c}$),
∵N(0,$\frac{t}{2}$),
∵|OE|=2|ON|,
∴2|$\frac{t}{2}$|=|$\frac{ta}{a-c}$|,
即c=2a,
则离心率e=$\frac{c}{a}$=2,
故选:B
点评 本题主要考查双曲线离心率的计算,根据条件求出直线方程和点N,E的坐标是解决本题的关键.

练习册系列答案
相关题目
8.已知定义在(0,+∞)的函数f(x)=|4x(1-x)|,若关于x的方程f2(x)+(t-3)f(x)+t-2=0有且只有3个不同的实数根,则实数t的取值集合是{2,$5-2\sqrt{2}$}.
9.函数y=|log3x|的图象与直线l1:y=m从左至右分别交于点A,B,与直线${l_2}:y=\frac{8}{2m+1}(m>0)$从左至右分别交于点C,D.记线段AC和BD在x轴上的投影长度分别为a,b,则$\frac{b}{a}$的最小值为( )
| A. | $81\sqrt{3}$ | B. | $27\sqrt{3}$ | C. | $9\sqrt{3}$ | D. | $3\sqrt{3}$ |
13.在《九章算术》中有一个古典名题“两鼠穿墙”问题:今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺.大鼠日自倍,小鼠日自半,问何日相逢?大意是有厚墙五尺,两只老鼠从墙的两边分别打洞穿墙.大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半,问几天后两鼠相遇?( )
| A. | 2$\frac{2}{17}$ | B. | 2$\frac{3}{17}$ | C. | 2$\frac{5}{17}$ | D. | 2.25 |
7.设集合A={x∈R|x-1>0},B={x∈R|x<0},C={x∈R|x(x-1)>0},则“x∈A∪B“是“x∈C“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
8.设函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{{x}^{2},x<0}\end{array}\right.$,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1,x2,则e${\;}^{{x}_{1}}$•e${\;}^{{x}_{2}}$的最大值为( )
| A. | $\frac{1}{{e}^{2}}$ | B. | 2(ln2-1) | C. | $\frac{4}{{e}^{2}}$ | D. | ln2-1 |
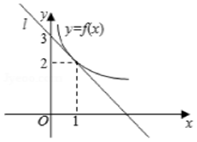 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.