题目内容
12.已知函数$f(x)+2=\frac{2}{{f(\sqrt{x+1})}}$,当x∈(0,1]时,f(x)=x2,若在区间(-1,1]内,g(x)=f(x)-t(x+1)有两个不同的零点,则实数t的取值范围是( )| A. | $[\frac{1}{2},+∞)$ | B. | $[-\frac{1}{2},\frac{1}{2}]$ | C. | $[-\frac{1}{2},0)$ | D. | $(0,\frac{1}{2}]$ |
分析 由g(x)=f(x)-t(x+1)=0得f(x)=t(x+1),分别求出函数f(x)的解析式以及两个函数的图象,利用数形结合进行求解即可.
解答 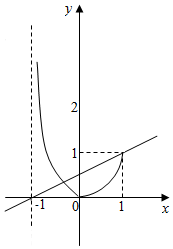 解:由题可知函数在x∈(-1,1]上的解析式为$f(x)=\left\{\begin{array}{l}\frac{-2x}{x+1}x∈(-1,0]\\{x^2}x∈(0,1]\end{array}\right.$,
解:由题可知函数在x∈(-1,1]上的解析式为$f(x)=\left\{\begin{array}{l}\frac{-2x}{x+1}x∈(-1,0]\\{x^2}x∈(0,1]\end{array}\right.$,
由g(x)=f(x)-t(x+1)=0得f(x)=t(x+1),
可将函数f(x)在x∈(-1,1)上的大致图象呈现如图:
根据y=t(x+1)的几何意义,x轴位置和图中直线位置为y=t(x+1)表示直线的临界位置,
因此直线的斜率t的取值范围是$(0,\frac{1}{2}]$.
故选:D.
点评 本题是最近热点的函数图象辨析问题,是一道较为复杂的难题.作出函数的图象,利用数形结合是解决本题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
20.在等差数列{an}中,a3+a5=12-a7,则a1+a9=( )
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
17.在一次数学考试中,数学课代表将他们班50名同学的考试成绩按如下方式进行统计得到如下频数分布表(满分为100分)
(Ⅰ)在答题卡上作出这些数据中的频率分布直方图;
(Ⅱ)估计该班学生数学成绩的中位数和平均值;
(Ⅲ)若按照学生成绩在区间[0,60),[60,80),[80,100)内,分别认定为不及格,及格,优良三个等次,用分层抽样的方法从中抽取一个容量为5的样本,计算:从该样本中任意抽取2名学生,至少有一名学生成绩属于及格等次的概率.
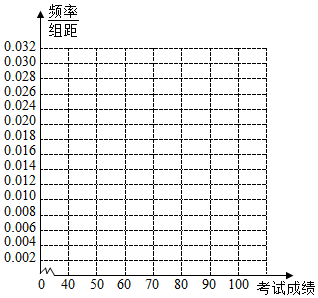
| 成绩 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 2 | 8 | 15 | 15 | 4 | 6 |
(Ⅱ)估计该班学生数学成绩的中位数和平均值;
(Ⅲ)若按照学生成绩在区间[0,60),[60,80),[80,100)内,分别认定为不及格,及格,优良三个等次,用分层抽样的方法从中抽取一个容量为5的样本,计算:从该样本中任意抽取2名学生,至少有一名学生成绩属于及格等次的概率.

4.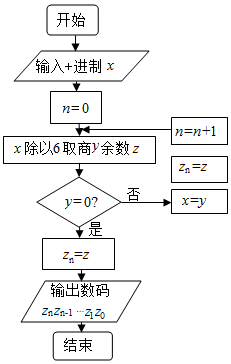 老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
 老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )| A. | 682 | B. | 683 | C. | 692 | D. | 693 |
1.已知θ∈(0,$\frac{π}{4}$),且sinθ-cosθ=-$\frac{\sqrt{14}}{4}$,则$\frac{2co{s}^{2}θ-1}{cos(\frac{π}{4}+θ)}$等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
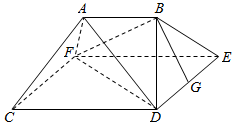 如图,在多面体ABCDEF中,四边形CDEF是正方形,AB∥CD,CD=2AB,G为DE的中点.
如图,在多面体ABCDEF中,四边形CDEF是正方形,AB∥CD,CD=2AB,G为DE的中点.