题目内容
1.已知θ∈(0,$\frac{π}{4}$),且sinθ-cosθ=-$\frac{\sqrt{14}}{4}$,则$\frac{2co{s}^{2}θ-1}{cos(\frac{π}{4}+θ)}$等于( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
分析 法1:由已知的等式记作①,利用同角三角函数间的基本关系列出关系式,记作②,再根据θ为锐角,联立①②求出sinθ和cosθ的值,进而利用二倍角的余弦函数公式及两角和与差的正弦函数公式分别求出所求式子的分子与分母,代入即可求出所求式子的值.
法2:利用两角和与差的三角函数化简已知条件以及所求表达式,通过同角三角函数基本关系式求解即可.
解答 解:法1:由sinθ-cosθ=-$\frac{\sqrt{14}}{4}$,①,
又sin2θ+cos2θ=1②,且θ∈(0,$\frac{π}{4}$),联立①②解得:sinθ=$\frac{3\sqrt{2}-\sqrt{14}}{8}$,cosθ=$\frac{\sqrt{14}+3\sqrt{2}}{8}$,
∴$\frac{2co{s}^{2}θ-1}{cos(\frac{π}{4}+θ)}$=$\sqrt{2}$(sinθ+cosθ)=$\sqrt{2}(\frac{3\sqrt{2}-\sqrt{14}}{8}+\frac{\sqrt{14}+3\sqrt{2}}{8})$=$\frac{3}{2}$.
故选:D.
法2:θ∈(0,$\frac{π}{4}$),且sinθ-cosθ=-$\frac{\sqrt{14}}{4}$,可得$\sqrt{2}$cos($θ+\frac{π}{4}$)=$\frac{\sqrt{14}}{4}$,即:cos($θ+\frac{π}{4}$)=$\frac{\sqrt{7}}{4}$,
$θ+\frac{π}{4}$∈($\frac{π}{4},\frac{π}{2}$),
则$\frac{2co{s}^{2}θ-1}{cos(\frac{π}{4}+θ)}$=$\frac{cos2θ}{cos(\frac{π}{4}+θ)}$=$\frac{2sin(\frac{π}{4}+θ)cos(\frac{π}{4}+θ)}{cos(\frac{π}{4}+θ)}$=2sin($θ+\frac{π}{4}$)=2$\sqrt{1-({\frac{\sqrt{7}}{4})}^{2}}$=$\frac{3}{2}$.
故选:D.
点评 此题考查了二倍角的余弦函数公式,两角和与差的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

| A. | $[\frac{1}{2},+∞)$ | B. | $[-\frac{1}{2},\frac{1}{2}]$ | C. | $[-\frac{1}{2},0)$ | D. | $(0,\frac{1}{2}]$ |
| A. | M⊆{x|x≥1} | B. | M⊆{x|x>-2} | C. | M∩N={0} | D. | M∪N=N |

| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
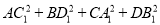 等于( )
等于( )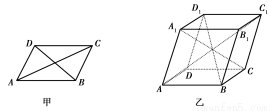
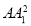 )
) 
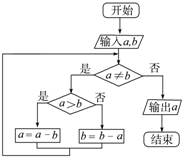 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,20,则输出的a=2.
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,20,则输出的a=2.