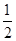题目内容
已知正三棱锥 的底面边长为4,高为3,在正三棱锥内任取一点
的底面边长为4,高为3,在正三棱锥内任取一点 ,使得
,使得 的概率是( )
的概率是( )
A. | B. | C. | D. |
A
解析试题分析:本题利用几何概型解决.根据题中条件: ”得点P所在的区域为棱锥的中截面以下,结合大棱锥与小棱锥的体积比即可求得结果。
”得点P所在的区域为棱锥的中截面以下,结合大棱锥与小棱锥的体积比即可求得结果。
由题意知,当点P在三棱锥的中截面以下时,满足 ,故使得
,故使得 的概率为P=
的概率为P= ,故选A
,故选A
考点:几何概型概率的求解
点评:本题主要考查了几何概型划,以及空间想象能力,属于基础题.简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型,解本题的关键是理解体积比是相似比的平方

练习册系列答案
相关题目
如图,△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PCB的大小( ).
| A.变大 | B.变小 | C.不变 | D.有时变大有时变小 |
在正方体 中,
中, ,
, 分别
分别 ,
, 是的中点,则下列判断错误的是
是的中点,则下列判断错误的是
A. 与 与 垂直 垂直 | B. 与 与 垂直 垂直 |
C. 与 与 平行 平行 | D. 与 与 平行 平行 |
 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,则下列命题中真命题的是( )
是三个不同的平面,则下列命题中真命题的是( )
A.若 ,则 ,则 | B.若  ,则 ,则 |
C.若 则 则 | D.若 ,则 ,则 |
已知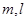 是两条不同的直线,
是两条不同的直线,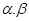 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题:
①若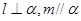 ,则
,则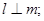 ②若
②若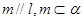 则
则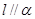 ;
;
③若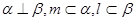 则
则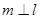 ; ④若
; ④若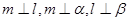 则
则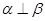 ;
;
其中正确命题的个数为 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知两个不同的平面 、
、 ,能判定
,能判定 //
// 的条件是( )
的条件是( )
A. 、 、 分别平行于直线 分别平行于直线 | B. 、 、 分别垂直于直线 分别垂直于直线 |
C. 、 、 分别垂直于平面 分别垂直于平面 | D. 内有两条直线分别平行于 内有两条直线分别平行于 |
已知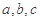 是三条不同的直线,
是三条不同的直线,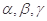 是三个不同的平面,下列命题中正确的是( )
是三个不同的平面,下列命题中正确的是( )
A.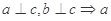 // //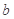 |
B.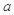 // //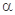 , ,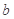 // //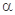 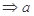 // //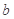 |
C.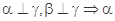 // //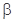 |
D.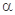 // //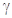 , ,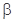 // //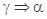 // //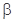 |
三棱锥 中,
中, ,
, 是等腰直角三角形,
是等腰直角三角形, .若
.若 为
为 中点,则
中点,则 与平面
与平面 所成的角的大小等于( )
所成的角的大小等于( )
A. | B. | C. | D. |
 一边BC在平面
一边BC在平面 内,顶点A在平面
内,顶点A在平面 ,三角形所在平面与
,三角形所在平面与 ,则直线
,则直线 与
与