题目内容
已知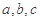 是三条不同的直线,
是三条不同的直线,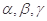 是三个不同的平面,下列命题中正确的是( )
是三个不同的平面,下列命题中正确的是( )
A.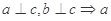 // //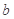 |
B.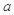 // //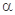 , ,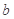 // //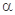 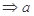 // //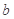 |
C.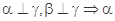 // //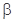 |
D.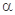 // //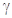 , ,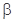 // //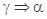 // //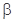 |
D
解析试题分析:因为a,b,c是空间直线,所以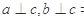 ,a,b的关系有三种:平行、相交、异面,A不正确;
,a,b的关系有三种:平行、相交、异面,A不正确;
因为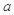 //
//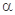 ,
,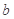 //
//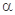 ,所以a//b或a,b相交或异面,B不正确;
,所以a//b或a,b相交或异面,B不正确;
根据墙角处三个墙面的关系可知,C不正确;
关系D。
考点:本题主要考查立体几何中的平行、垂直关系。
点评:基础题,立体几何中的平行关系、垂直关系是常考内容,注意牢记立体几何中的定理,并灵活运用。

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
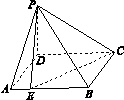
已知正三棱锥 的底面边长为4,高为3,在正三棱锥内任取一点
的底面边长为4,高为3,在正三棱锥内任取一点 ,使得
,使得 的概率是( )
的概率是( )
A. | B. | C. | D. |
正方体 中,直线
中,直线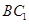 与
与 ( )
( )
| A.异面且垂直 | B.异面但不垂直 |
| C.相交且垂直 | D.相交但不垂直 |
设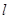 ,
,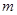 是两条不同的直线,
是两条不同的直线,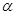 是一个平面,则下列命题正确的是 ( )
是一个平面,则下列命题正确的是 ( )
A.若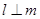 , ,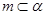 ,则 ,则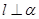 | B.若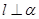 , ,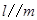 ,则 ,则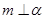 |
C.若 , ,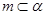 ,则 ,则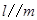 | D.若 , ,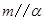 ,则 ,则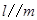 |
下列命题中,错误的命题是( )
| A.平行于同一直线的两个平面平行。 |
| B.一条直线与两个平行平面中的一个相交,那么这条直线必和另一个平面相交。 |
| C.平行于同一平面的两个平面平行。 |
| D.一条直线与两个平行平面所成的角相等。 |
若a,b是异面直线,且a∥平面α,则b和α的位置关系是( )
| A.平行 | B.相交 |
| C.b在α内 | D.平行、相交或b在α内 |
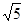
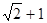
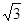
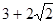
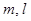 ,平面
,平面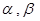 ,且
,且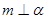 ,
,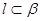 ,给出下列命题
,给出下列命题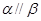 ,则
,则 (2)若
(2)若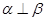 ,则
,则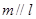
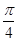 时,AE=( )
时,AE=( )