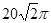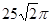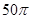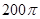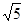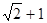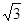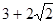题目内容
△ 一边BC在平面
一边BC在平面 内,顶点A在平面
内,顶点A在平面 外,已知
外,已知 ,三角形所在平面与
,三角形所在平面与 所成的二面角为
所成的二面角为 ,则直线
,则直线 与
与 所成角的正弦值为( )
所成角的正弦值为( )
A. | B. | C.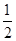 | D. |
D
解析试题分析:根据已知条件画图(如图)
图中AD⊥BC,HD⊥BC,AH⊥α,∠ABC=60°,∠ADH=30°,
所以∠ABH即为AB与α所成角,则AD= AB,AH=
AB,AH=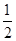 AD,AH=
AD,AH= AB,
AB,
sin∠ABH= =
= ,故选D.
,故选D.
考点:本题主要考查立体几何中的垂直关系及角的计算。
点评:典型题,立体几何问题中,平行关系、垂直关系、角的计算、距离的计算、面积的计算、体积计算等,是高考常考内容。就计算问题而言,“几何法”要遵循“一作、二证、三计算”。

练习册系列答案
相关题目
设 是直线,
是直线, 是两个不同的平面,下列命题成立的是( )
是两个不同的平面,下列命题成立的是( )
A.若 ,则 ,则 |
B.若 ∥ ∥ ,则 ,则 |
C.若 ∥ ∥ , , , 则 , 则 ∥ ∥ |
D.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
已知正三棱锥 的底面边长为4,高为3,在正三棱锥内任取一点
的底面边长为4,高为3,在正三棱锥内任取一点 ,使得
,使得 的概率是( )
的概率是( )
A. | B. | C. | D. |
如图:正方体 中,
中, 与
与 所成的角为( )
所成的角为( )
A. | B. | C. | D. |
在三棱柱 中,各棱长相等,侧掕垂直于底面,点
中,各棱长相等,侧掕垂直于底面,点 是侧面
是侧面 的中心,则
的中心,则 与平面
与平面 所成角的大小是 ( )
所成角的大小是 ( )
A.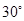 | B.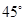 | C. | D. |
正方体 中,直线
中,直线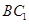 与
与 ( )
( )
| A.异面且垂直 | B.异面但不垂直 |
| C.相交且垂直 | D.相交但不垂直 |
下列命题中,错误的命题是( )
| A.平行于同一直线的两个平面平行。 |
| B.一条直线与两个平行平面中的一个相交,那么这条直线必和另一个平面相交。 |
| C.平行于同一平面的两个平面平行。 |
| D.一条直线与两个平行平面所成的角相等。 |