题目内容
如图,△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PCB的大小( ).
| A.变大 | B.变小 | C.不变 | D.有时变大有时变小 |
C
解析试题分析:因为∠ACB=90°,所以AC⊥BC,又因为直线l垂直于平面ABC,所以l⊥BC,根据线面垂直的判定定理可知,BC⊥平面PAC,所以∠PCB=90°,即∠PCB的大小不变.
考点:本小题主要考查线面垂直的判定和应用.
点评:应用线面垂直的判定定理时要注意直线要垂直于平面内的两条相交直线.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列四个命题中,正确命题的个数是( )
是两个不同的平面,则下列四个命题中,正确命题的个数是( )
①若 ②若
②若
③若 ④若
④若
| A.3个 | B.2个 | C.1个 | D.0个 |
下列命题中假命题是
| A.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 |
| B.垂直于同一条直线的两条直线相互垂直 |
| C.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 |
| D.若一个平面内的两条相交直线与另一个平面内的相交直线分别平行,那么这两个平面相互平行 |
已知 是两两不重合的三个平面,下列命题中错误的是( )
是两两不重合的三个平面,下列命题中错误的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
已知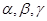 是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①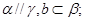 ②
②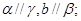 ③
③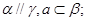 如果命题
如果命题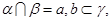 且_______,则
且_______,则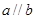 为真命题,则可以在横线处填入的条件是( )
为真命题,则可以在横线处填入的条件是( )
| A.①或② | B.②或③ | C.①或③ | D.只有② |
对于两条不相交的空间直线 和
和 ,必定存在平面
,必定存在平面 ,使得 ( )
,使得 ( )
A. | B. | C. | D. |
设、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , ,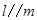 ,则 ,则 |
C.若 , , ,则 ,则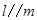 | D.若 , , ,则 ,则 |
设 是直线,
是直线, 是两个不同的平面,下列命题成立的是( )
是两个不同的平面,下列命题成立的是( )
A.若 ,则 ,则 |
B.若 ∥ ∥ ,则 ,则 |
C.若 ∥ ∥ , , , 则 , 则 ∥ ∥ |
D.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
已知正三棱锥 的底面边长为4,高为3,在正三棱锥内任取一点
的底面边长为4,高为3,在正三棱锥内任取一点 ,使得
,使得 的概率是( )
的概率是( )
A. | B. | C. | D. |