题目内容
16.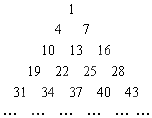 将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )
将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )| A. | 571 | B. | 574 | C. | 577 | D. | 580 |
分析 设各行的首项组成数列{an},则a2-a1=3,a3-a2=6,…,an-an-1=3(n-1),叠加可得:an=$\frac{3n(n-1)}{2}$+1,由此可求数阵中第20行从左至右的第3个数.
解答 解:设各行的首项组成数列{an},则a2-a1=3,a3-a2=6,…,an-an-1=3(n-1)
叠加可得:an-a1=3+6+…+3(n-1)=$\frac{3n(n-1)}{2}$,
∴an=$\frac{3n(n-1)}{2}$+1
∴a20=$\frac{3×20×19}{2}$+1=571
∴数阵中第20行从左至右的第3个数是577.
故选:C.
点评 本题考查归纳推理,考查数列的特点,观察分析数字的排列规律是解题的关键.

练习册系列答案
相关题目
4.设随机变量ξ的分布列为p(ξ=k)=$\frac{k}{3a}$(k=1,2,3,4,5),则p(ξ≤2)等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{15}$ | D. | $\frac{2}{15}$ |
11.已知圆${x^2}+{y^2}+(4-2a)x-2\sqrt{3}ay+4{a^2}-4a-12=0$,定直线l经过点A(1,0),若对任意的实数a,定直线l被圆C截得的弦长始终为定值d,求得此定值d等于( )
| A. | $2\sqrt{7}$ | B. | $\sqrt{31}$ | C. | $\sqrt{34}$ | D. | $\sqrt{37}$ |
8.如图所示,程序据图(算法流程图)的输出结果为( )
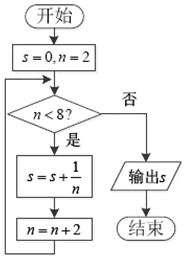

| A. | $\frac{3}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{11}{12}$ | D. | $\frac{25}{24}$ |
5.f(x)为奇函数,且x>0时,f(x)=x2-2x,则x<0时,f(x)=( )
| A. | f(x)=x2+2-x | B. | f(x)=x2-2-x | C. | f(x)=-x2+2-x | D. | f(x)=-x2-2-x |
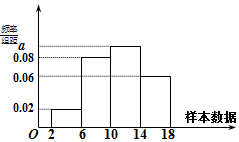 如图是容量为100的样本的频率分布直方图,其中a∈R.试根据图中的数据回答下列问题:
如图是容量为100的样本的频率分布直方图,其中a∈R.试根据图中的数据回答下列问题:


