题目内容
1．若函数f（x）=ax（a＞0，且a≠1），若$f（2）=\frac{1}{4}$，则函数y=loga|x|的图象大致是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据函数f（x）=ax，$f（2）=\frac{1}{4}$，可得a值，结合对数函数的图象和性质，函数图象的对折变换法则，可得答案．
解答 解：∵函数f（x）=ax，$f（2）=\frac{1}{4}$，
∴a=$\frac{1}{2}$，
故函数y=loga|x|的图象关于y轴对称，
且在（0，+∞）上为减函数，
故选：A．
点评 本题考查的知识点是函数的图象，指数函数的图象和性质，对数函数的图象和性质，难度中档．
练习册系列答案
考前必练系列答案
相关题目
12．已知 an=$\frac{n-1}{n+1}$，那么数列{an}是（ ）
| A． | 递减数列 | B． | 递增数列 | C． | 常数列 | D． | 摆动数列 |
9．如果直线ax+2y+2=0与直线3x-y-2=0互相垂直，那么实数a=（ ）
| A． | $\frac{2}{3}$ | B． | $-\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | 6 |
16．
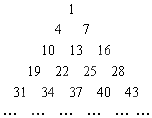将等差数列1，4，7…，按一定的规则排成了如图所示的三角形数阵．根据这个排列规则，数阵中第20行从左至右的第3个数是（ ）
将等差数列1，4，7…，按一定的规则排成了如图所示的三角形数阵．根据这个排列规则，数阵中第20行从左至右的第3个数是（ ）| A． | 571 | B． | 574 | C． | 577 | D． | 580 |
13．当x∈[1，2]时，函数f（x）=2x-1的值域为（ ）
| A． | [-3，-1] | B． | [1，3] | C． | [-1，2] | D． | [-1，1] |