题目内容
4.设随机变量ξ的分布列为p(ξ=k)=$\frac{k}{3a}$(k=1,2,3,4,5),则p(ξ≤2)等于( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{15}$ | D. | $\frac{2}{15}$ |
分析 由随机变量ξ的分布列的性质求出a=5,再由P(ξ≤2)=P(ξ=1)+P(ξ=2),能求出结果.
解答 解:∵随机变量ξ的分布列为p(ξ=k)=$\frac{k}{3a}$(k=1,2,3,4,5),
∴$\frac{1+2+3+4+5}{3a}$=1,
解得a=5,
∴P(ξ≤2)=P(ξ=1)+P(ξ=2)=$\frac{1+2}{15}$=$\frac{1}{5}$,
故选A.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意离散型随机变量的分布列的性质的合理运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
12.已知 an=$\frac{n-1}{n+1}$,那么数列{an}是( )
| A. | 递减数列 | B. | 递增数列 | C. | 常数列 | D. | 摆动数列 |
19.定积分${∫}_{0}^{2}$(-3)dx等于( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
9.如果直线ax+2y+2=0与直线3x-y-2=0互相垂直,那么实数a=( )
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 6 |
16.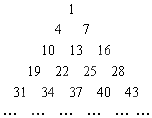 将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )
将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )
 将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )
将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )| A. | 571 | B. | 574 | C. | 577 | D. | 580 |
13.当x∈[1,2]时,函数f(x)=2x-1的值域为( )
| A. | [-3,-1] | B. | [1,3] | C. | [-1,2] | D. | [-1,1] |
14.已知m.n是空间两条不同的直线,α是一个平面,则下列命题为假命题的是( )
| A. | m⊥α,n∥α⇒m⊥n | B. | m⊥α,n⊥α⇒m∥n | ||
| C. | m⊥α,n⊥m⇒n∥α或n?α | D. | m∥α,n⊥m⇒n⊥α或n∥α或n?α |
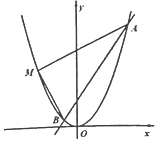 已知抛物线x2=2py(p>0)与直线2x-y+1=0交于A,B两点,$|AB|=2\sqrt{30}$,点M在抛物线上,MA⊥MB.
已知抛物线x2=2py(p>0)与直线2x-y+1=0交于A,B两点,$|AB|=2\sqrt{30}$,点M在抛物线上,MA⊥MB.