题目内容
15.$f(x)=2\sqrt{3}sinx-2cosx$,则f(x)的最大值为4.分析 利用辅助角公式化简函数为一个角的一个三角函数的形式,利用正弦函数的最值求解即可.
解答 解:$f(x)=2\sqrt{3}sinx-2cosx$=4($\frac{\sqrt{3}}{2}$sinα-$\frac{1}{2}$cosα)=4sin(x-$\frac{π}{6}$)≤4,
所以函数的最大值为:4.
故答案为:4.
点评 本题考查三角函数的最值,辅助角个数的应用,考查计算能力.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
6.已知函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的最小正周期是π,函数图象过点P(0,1),则函数f(x)=sin(ωx+φ)( )
| A. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 | B. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增 | ||
| C. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递减 | D. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递增 |
3.下列结论①(sinx)′=-cosx;②$(\frac{1}{x})'=\frac{1}{x^2}$;③$({log_3}x)'=\frac{1}{3lnx}$;④$({x^2})'=\frac{1}{x}$.其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10.已知f(x)=lg(x-1),则f(x+3)=( )
| A. | lg(x+1) | B. | lg(x+2) | C. | lg(x+3) | D. | lg(x+4) |
7.若a+2b=1(ab≠0),下列结论中错误的是( )
| A. | ab的最大值为$\frac{1}{8}$ | B. | $\frac{1}{ab}$的最小值为8 | ||
| C. | a2+ab+b2的最小值为$\frac{1}{4}$ | D. | $\frac{1}{{{a^2}+ab+{b^2}}}$的最大值为4 |
 定义:如果两个椭圆的离心率相等,那么称这两个椭圆相似,它们的长轴长之比(大于1)叫做这两个椭圆的相似比.(1)设m,n∈N*,试判断椭圆C1:$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{m}$=1和椭圆C2:$\frac{{x}^{2}}{m+n}$+$\frac{{y}^{2}}{m+1}$=1能否相似?若能,求出它们的相似比;若不能,请说明理由.
定义:如果两个椭圆的离心率相等,那么称这两个椭圆相似,它们的长轴长之比(大于1)叫做这两个椭圆的相似比.(1)设m,n∈N*,试判断椭圆C1:$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{m}$=1和椭圆C2:$\frac{{x}^{2}}{m+n}$+$\frac{{y}^{2}}{m+1}$=1能否相似?若能,求出它们的相似比;若不能,请说明理由.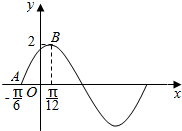 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示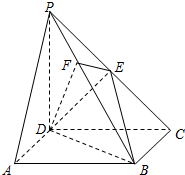 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.