题目内容
7.在△ABC中,$∠ABC=\frac{2π}{3}$,过B点作BD⊥AB交AC于点D.若AB=CD=1,则AD=$\root{3}{2}$.分析 设AD=x,由题意求出∠CBD、sin∠BDC,由正弦定理求出BC,在△ABC中由余弦定理列出方程,化简后求出x的值,可得答案.
解答 解:设AD=x,且BD⊥AB,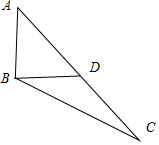 AB=CD=1,
AB=CD=1,
在△BCD中,$∠ABC=\frac{2π}{3}$,则$∠CBD=\frac{π}{6}$,
且sin∠BDC=sin(π-∠ADB)=sin∠ADB=$\frac{AB}{AD}$=$\frac{1}{x}$,
由正弦定理得,$\frac{BC}{sin∠BDC}=\frac{CD}{sin∠CBD}$,
所以BC=$\frac{CD•sin∠BDC}{sin∠CBD}$=$\frac{1×\frac{1}{x}}{\frac{1}{2}}$=$\frac{2}{x}$,
在△ABC中,由余弦定理得,
AC2=AB2+BC2-2•AB•BCcos∠ABC
则${(1+x)}^{2}=1+(\frac{2}{x})-2×1×\frac{2}{x}×(-\frac{1}{2})$,化简得,${x}^{2}+2x=\frac{2x+4}{{x}^{2}}$,
解得x=$\root{3}{2}$,即AD=$\root{3}{2}$,
故答案为:$\root{3}{2}$.
点评 本题考查正弦定理,余弦定理的应用,考查方程思想,化简、计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知点P(t,t-1),t∈R,点E是圆x2+y2=$\frac{1}{4}$上的动点,点F是圆(x-3)2+(y+1)2=$\frac{9}{4}$上的动点,则|PF|-|PE|的最大值为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
2.若$tanθ=-\frac{1}{3},θ∈(\frac{π}{2},π),则cos2θ$=( )
| A. | $-\frac{4}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
16.已知函数$y=3sin(ωx+\frac{π}{3})$的最小正周期为π,将函数$y=3sin(ωx+\frac{π}{3})$的图象向右平移$\frac{π}{2}$个单位长度,所得图象对应的函数( )
| A. | 在区间$[\frac{π}{12},\frac{7π}{12}]$上单调递减 | B. | 在区间$[\frac{π}{12},\frac{7π}{12}]$上单调递增 | ||
| C. | 在区间$[-\frac{π}{6},\frac{π}{3}]$上单调递减 | D. | 在区间$[-\frac{π}{6},\frac{π}{3}]$上单调递增 |