题目内容
6.若函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<$\frac{π}{2}$)在其中一个周期内的图象上有一个最高点($\frac{π}{12}$,3)和一个最低点($\frac{7π}{12}$,-5),求该函数的解析式.分析 由函数的图象的顶点坐标求出A,b,由周期求出ω,由顶点的坐标求出φ的值.
解答 解:由题意可知:$\left\{\begin{array}{l}{A+b=3}\\{-A+b=-5}\end{array}\right.$,解得:A=4,b=-1,
∵$\frac{T}{2}$=$\frac{7π}{12}$-$\frac{π}{12}$=$\frac{π}{2}$,可得:T=π=$\frac{2π}{ω}$,求得ω=2.
再根据最高点的坐标可得2×$\frac{π}{12}$+φ=$\frac{π}{2}$+2kπ,k∈Z,
∴φ=$\frac{π}{3}$+2kπ,k∈Z.
结合|φ|<$\frac{π}{2}$,可得φ=$\frac{π}{3}$.
可得该函数的解析式为:y=4sin(2x+$\frac{π}{3}$)-1.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由顶点的坐标求出φ的值,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.一个正三棱柱的主(正)视图是长为2$\sqrt{3}$,宽为4的矩形,则它的外接球的表面积等于( )
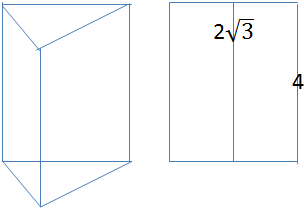

| A. | 64π | B. | 48π | C. | 32π | D. | 16π |
 在
在 上单调递增,则
上单调递增,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 ,集合
,集合 ,则( )
,则( ) B.
B.
 D.
D.