题目内容
1.命题p:若“?x0∈[0,$\frac{π}{4}$],tanx0>m-3”是假命题,则实数m的最小值为4.分析 若命题p:若“?x0∈[0,$\frac{π}{4}$],tanx0>m-3”是假命题,则命题¬p:若“?x∈[0,$\frac{π}{4}$],tanx≤m-3”是真命题,故1≤m-3,解得答案.
解答 解:若命题p:若“?x0∈[0,$\frac{π}{4}$],tanx0>m-3”是假命题,
则命题¬p:若“?x∈[0,$\frac{π}{4}$],tanx≤m-3”是真命题,
故1≤m-3,
解得:m≥4,
即实数m的最小值为4,
故答案为:4.
点评 本题以命题的真假判断与应用为载体,考查了特称命题,恒成立问题,正切函数的图象和性质,难度中档.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
12.若f(x)=$\left\{{\begin{array}{l}{{a^x},x<0}\\{{{log}_a}x,x>0}\end{array}}$,那么y=f(x)-a的零点个数有( )
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | a的值不同时零点的个数不同 |
12.随机变量X的分布列如下:若E(X)=$\frac{15}{8}$,则D(X)等于( )
| X | 1 | 2 | 3 |
| P | 0.5 | x | y |
| A. | $\frac{7}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{33}{64}$ | D. | $\frac{55}{64}$ |
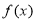 和
和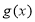 分别是
分别是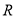 上的偶函数和奇函数,则下列结论恒成立的是( )
上的偶函数和奇函数,则下列结论恒成立的是( )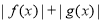 是偶函数 B.
是偶函数 B.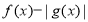 是奇函数
是奇函数 是偶函数 D.
是偶函数 D.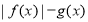 是奇函数
是奇函数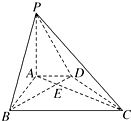 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2$\sqrt{3}$,BC=6.
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2$\sqrt{3}$,BC=6.