题目内容
6.要得到函数y=3sin2x(x∈R)的图象,只要将函数y=3sin(2x+1)(x∈R)的图象( )| A. | 向左平移1个位长度,纵坐标不变 | B. | 向右平移1个位长度,纵坐标不变 | ||
| C. | 向左平移$\frac{1}{2}$个位长度,纵坐标不变 | D. | 向右平移$\frac{1}{2}$个位长度,纵坐标不变 |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:只要将函数y=3sin(2x+1)(x∈R)的图象,向右平移$\frac{1}{2}$个位长度,纵坐标不变,
即可得到函数y═3sin[2(x-$\frac{1}{2}$+1]=3sin2x(x∈R)的图象,
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
15.已知数列{an}满足a1=-1,|an-an-1|=2n-1(n∈N,n≥2),且{a2n-1}是递减数列,{a2n}是递增数列,则a2016=$\frac{{2}^{2016}-1}{3}$.
16.设a,b∈R,则“a>b”是“a(ea+e-a)>b(eb+e-b)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要 条件 |
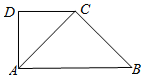 已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.
已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.